题目内容
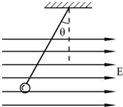如图所示，用一根绝缘细线悬挂一个带电小球，小球的质量为m，电量为q，现加一水平方向的匀强电场，平衡时绝缘细线与竖直方向夹θ角．求：（1）匀强电场的场强E大小是多少？
（2）如果将电场方向顺时针旋转θ角、大小变为E′后，小球平衡时，绝缘细线仍与竖直方向夹θ角，则E′的大小又是多少？
分析：（1）对小球受力分析，受到重力、电场力和细线的拉力，根据共点力平衡条件和电场力F=qE列式求解场强E．
（2）如果将电场方向顺时针旋转θ角、大小变为E′后，电场力方向也顺时针转过θ角，大小为F′=qE′，再运用同样的方法求解E′的大小．
（2）如果将电场方向顺时针旋转θ角、大小变为E′后，电场力方向也顺时针转过θ角，大小为F′=qE′，再运用同样的方法求解E′的大小．
解答：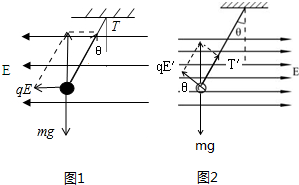
解：（1）对小球受力分析，受到重力、电场力和细线的拉力，如图．
由平衡条件得：
mgtanθ=qE
解得，E=
（2）将电场方向顺时针旋转θ角、大小变为E′后，电场力方向也顺时针转过θ角，大小为F′=qE′，此时电场力与细线垂直，如图所示．
根据平衡条件得：mgsinθ=qE′
则得 E′=
．
答：
（1）匀强电场的场强E大小是
．
（2）如果将电场方向顺时针旋转θ角、大小变为E′后，小球平衡时，绝缘细线仍与竖直方向夹θ角，则E′的大小是
．
解：（1）对小球受力分析，受到重力、电场力和细线的拉力，如图．由平衡条件得：
mgtanθ=qE
解得，E=
| mgtanθ |
| q |
（2）将电场方向顺时针旋转θ角、大小变为E′后，电场力方向也顺时针转过θ角，大小为F′=qE′，此时电场力与细线垂直，如图所示．
根据平衡条件得：mgsinθ=qE′
则得 E′=
| mgsinθ |
| q |
答：
（1）匀强电场的场强E大小是
| mgtanθ |
| q |
（2）如果将电场方向顺时针旋转θ角、大小变为E′后，小球平衡时，绝缘细线仍与竖直方向夹θ角，则E′的大小是
| mgsinθ |
| q |
点评：本题关键是对小球受力分析，然后根据共点力平衡条件，运用通过合成法求解．
练习册系列答案
相关题目
如图所示，用一根绝缘轻绳悬挂一个带电小球，小球的质量为m=1.0×10-2kg．现加一水平方向向左的匀强电场，场强E=3.0×106N/C，平衡时绝缘线与竖直方向的夹角θ为30°．
如图所示，用一根绝缘细线悬挂一个带电小球，小球的质量为m，电量为q，现加一水平的匀强电场，平衡时绝缘细线与竖直方向夹θ角，该小球带
（2008?岳阳二模）如图所示，用一根绝缘轻绳悬挂一个带电小球，小球的质量为1.0×10-2kg，所带电荷量为-2.0×10-8C．现加一水平方向的匀强电场，平衡时绝缘绳与竖直方向成30°角，g=10m/s2．则（ ）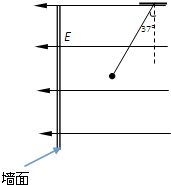
如图所示，用一根绝缘轻绳悬挂一个带电小球，小球的质量为m=1.0×10-2