题目内容
6. 如图所示,水平传送带的右端与竖直面内的用光滑钢管弯成的“9”形固定轨道相接,钢管内径很小.传送带的运行速度为v0=6m/s,将质量m=1.0kg的可看作质点的滑块无初速地放到传送带A端,传送带长度为L=12.0m,“9”字全高H=0.8m,“9”字上半部分圆弧半径为R=0.2m,滑块与传送带间的动摩擦因数为μ=0.3,重力加速g=10m/s2,试求:
如图所示,水平传送带的右端与竖直面内的用光滑钢管弯成的“9”形固定轨道相接,钢管内径很小.传送带的运行速度为v0=6m/s,将质量m=1.0kg的可看作质点的滑块无初速地放到传送带A端,传送带长度为L=12.0m,“9”字全高H=0.8m,“9”字上半部分圆弧半径为R=0.2m,滑块与传送带间的动摩擦因数为μ=0.3,重力加速g=10m/s2,试求:(1)滑块从传送带A 端运动到B 端所需要的时间;
(2)滑块滑到轨道最高点C时对轨道作用力的大小和方向;
(3)若滑块从“9”形轨道D点水平抛出后,恰好垂直撞在倾角θ=45°的斜面上P点,求P、D 两点间的竖直高度 h(保留两位有效数字).
分析 (1)滑块在传送带上先加速后匀速,根据牛顿第二定律求加速度,然后根据运动学公式求加速时间和位移,再求匀速时间,得到总时间;
(2)先对从B到C过程根据机械能守恒定律求出C点速度,再根据重力和轨道作用力的合力提供向心力,列方程求出轨道的作用力,再得到滑块对轨道的作用力;
(3)滑块从B到D的过程中由动能定理列式求滑块经过D点的速度.根据滑块垂直撞在倾角θ=45°的斜面上P点,由速度的分解求出竖直分竖直速度,再求h.
解答 解:(1)在传送带上加速运动时,由牛顿第二定律得:μmg=ma,
得:a=μg=0.3×10m/s2=3m/s2
加速到与传送带达到共速所需要的时间为:t1=$\frac{{v}_{0}}{a}$=$\frac{6}{3}$=2s
前2s内的位移为:x1=$\frac{1}{2}a{t}_{1}^{2}$=$\frac{1}{2}×3×{2}^{2}$m=6m
之后滑块做匀速运动的位移为:x2=L-x1=6m
所用的时间为:t2=$\frac{{x}_{2}}{{v}_{0}}$=$\frac{6}{6}$s=1s
故滑块从传送带A 端运动到B 端所需要的时间:t=t1+t2=3s
(2)滑块由B到C的过程中动能定理得:
-mgH=$\frac{1}{2}m{v}_{C}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
在C点,轨道对滑块的弹力与其重力的合力为其做圆周运动提供向心力,设轨道对滑块的弹力方向竖直向下,由牛顿第二定律得:
FN+mg=m$\frac{{v}_{C}^{2}}{R}$
联立并代入数据解得:FN=m$\frac{{v}_{0}^{2}}{R}$-mg($\frac{2H}{R}$+1)=90N,方向竖直向下
由牛顿第三定律得,滑块对轨道的压力大小 90N,方向竖直向上.
(3)滑块从B到D的过程中由动能定理得:
-mg(H-2R)=$\frac{1}{2}m{v}_{D}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
在P点竖直分速度为:vy=$\frac{{v}_{D}}{tan45°}$,又h=$\frac{{v}_{y}^{2}}{2g}$,
代入数据解得:h=1.4m
答:(1)滑块从传送带A端运动到B端所需要的时间为3s;
(2)滑块滑到轨道最高点C时对轨道作用力的大小为90N和方向竖直向上.
(3)P、D 两点间的竖直高度 h是1.4m.
点评 本题中物体在传送带上先加速后匀速运动,根据牛顿第二定律和运动学公式联立确定运动情况,滑块在细管中运动时机械能守恒,可以求出各个时刻的速度,最后结合平抛运动的规律解答.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | $\frac{3F}{16}$ | B. | $\frac{3F}{32}$ | C. | 0 | D. | $\frac{3F}{64}$ |
| A. | 减少50W | B. | 减少1200W | C. | 减少7.68×105W | D. | 减小78.13W |
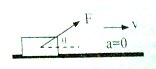 质量为m的物体与水平地面之间的动摩擦因数为μ,在斜向上、与水平方向夹角为θ的拉力F作用下,物体沿着水平地面做匀速直线运动.
质量为m的物体与水平地面之间的动摩擦因数为μ,在斜向上、与水平方向夹角为θ的拉力F作用下,物体沿着水平地面做匀速直线运动.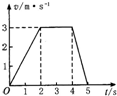 如图是质点运动的v-t图象,该质点在0~2s内的加速度是1.5m/s2,4~5s内的加速度是-3m/s2.
如图是质点运动的v-t图象,该质点在0~2s内的加速度是1.5m/s2,4~5s内的加速度是-3m/s2.