题目内容
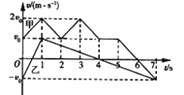
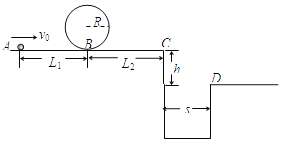
【题目】如图所示,一小球从A点以某一水平向右的初速度出发,沿水平直线轨道运动到B点后,进入半径R=10cm的光滑树枝圆形轨道,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续向C点右侧有一壕沟,C、D两点的竖直高度h=0.8cm,水平距离s=1.2cm,水平轨道AB长为L1=1m,BC长为L2=3m.小球与水平轨道间的动摩擦因数u=0.2,重力加速度g=10m/s2,重力加速度g=10m/s2,则:
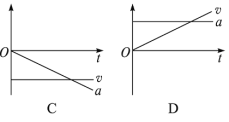
(1)若小球恰能通过圆形轨道的最高点,求小球在A点的初速度?
(2)若小球既能通过圆形轨道的最高点,又不能掉进壕沟,求小球在A点的初速度的范围是多少?
【答案】(1)3m/s(2)vA≥5m/s
【解析】试题分析:(1)小球恰能通过最高点![]() ①
①
由B到最高点![]() ②
②
由A→B![]() ③
③
解得:在A点的初速度vA=3m/s ④
(2)若小球恰好停在C处,对全程进行研究,则有:﹣μmg(L+L′)=0﹣![]() ,解得v′=4m/s.
,解得v′=4m/s.
所以当3m/s≤vA≤4m/s时,小球停在BC间.
若小球恰能越过壕沟时,则有h=![]() gt2,s=vt,又﹣μmg(L+L′)=
gt2,s=vt,又﹣μmg(L+L′)=![]()
解得,v″=5m/s
所以当vA≥5m/s,小球越过壕沟.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在研究匀变速直线运动的实验中,算出小车经过各计数点瞬时速度如下:
计数点序号 | 1 | 2 | 3 | 4 | 5 | 6 |
计数点对应的时刻(s) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
通过计数点的速度(cm/s) | 44.0 | 62.0 | 81.0 | 100.0 | 110.0 | 168.0 |
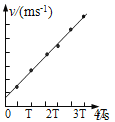
为了计算加速度,最合理的方法是( )
A.根据任意两计数点的速度用公式![]() 算出加速度
算出加速度
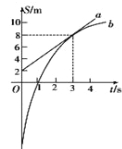
B.根据实验数据画出v-t图,量出其倾角θ,由公式a=tanθ求出加速度
C.根据实验数据画出v-t图,由图线上相距较远的两点所对应的速度、时间,用公式![]() 算出加速度
算出加速度
D.依次算出通过连续两计数点间的加速度,即![]() 、
、![]() 、………,然后算出平均值
、………,然后算出平均值![]() 作为小车的加速度
作为小车的加速度