题目内容
如图所示，在方向垂直向里，磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd，线框以恒定的速度v沿垂直磁场方向向右运动，运动中线框dc边始终与磁场右边界平行，线框边长ad=l，cd=2l．线框导线的总电阻为R．则线框离开磁场的过程中，流过线框截面的电量为| 2Bl2 |
| R |
| 2Bl2 |
| R |
| 4Blv |
| 3 |
| 4Blv |
| 3 |
| 2l3B2v |
| 3R |
| 2l3B2v |
| 3R |
分析：根据感应电量q=
，分析磁通量变化量关系，来求解感应电量．分析线框的受力情况，线框所受安培力的合力．
ab间的电压，为路段电压，即为bc、cd、ad间的总电压．
根据焦耳定律求解电流在ad边产生的热量．
| △Φ |
| R |
ab间的电压，为路段电压，即为bc、cd、ad间的总电压．
根据焦耳定律求解电流在ad边产生的热量．
解答：解：线框离开磁场的过程中，ab边在切割磁感线，ab边相当于电源，
则产生的感应电动势：E=2Blv，
所以电路中的电流：I=
=
，
相框的总电阻为R，根据电阻定律可知：
ab边的电阻等于cd边的电阻为
bc边的电阻等于ad边的电阻为
1、根据电流的定义式I=
，可得流过线框截面的电量q=It=
t=
t=
=
=
．
2、ab间的电压，为路段电压，即为bc、cd、ad间的总电压，Uab=I?(
+
+
)=
．
3、线框中的电流在ad边产生的热量：Q=I2?
R?
=
．
故答案为：
，
，
．
则产生的感应电动势：E=2Blv，
所以电路中的电流：I=
| E |
| R |
| 2Blv |
| R |
相框的总电阻为R，根据电阻定律可知：
ab边的电阻等于cd边的电阻为
| R |
| 3 |
bc边的电阻等于ad边的电阻为
| R |
| 6 |
1、根据电流的定义式I=
| q |
| t |
| E |
| R |
| △Φ |
| △t?R |
| △Φ |
| R |
| B?(l?2l) |
| R |
| 2Bl2 |
| R |
2、ab间的电压，为路段电压，即为bc、cd、ad间的总电压，Uab=I?(
| R |
| 3 |
| R |
| 6 |
| R |
| 6 |
| 4Blv |
| 3 |
3、线框中的电流在ad边产生的热量：Q=I2?
| 1 |
| 6 |
| l |
| v |
| 2l3B2v |
| 3R |
故答案为：
| 2Bl2 |
| R |
| 4Blv |
| 3 |
| 2l3B2v |
| 3R |
点评：该题考查了法拉第电磁感应定律和闭合回路欧姆定律的应用，是一道常规题．要注意题目中线框边长不等，分清楚哪个边在切割磁感线．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
如图所示，在方向垂直纸面向里，磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd，线框以恒定的速度v沿垂直磁场方向向右运动，运动中线框dc边始终与磁场右边界平行，线框边长ad=l，cd=2l．线框导线的总电阻为R．则线框离开磁场的过程中（ ）
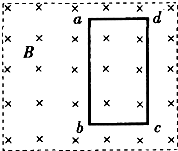如图所示，在方向垂直于纸面向里，磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd，线框在水平拉力作用下以恒定的速度v沿垂直磁场方向向右运动，运动中线框ab边始终与磁场右边界平行，线框边长ad=l，cd=2l，线框导线的总电阻为R．则线框离开磁场的过程中（ ）A、ab间的电压为
| ||
B、ad间的电压为
| ||
C、线框中的电流在ab边产生的热量为
| ||
D、线框中的电流在ad边产生的热量为
|
如图所示，在方向垂直向里，磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd，线框在水平拉力作用下以恒定的速度v沿垂直磁场方向向右运动，运动中线框dc边始终与磁场右边界平行，线框边长ad＝l，cd＝2l。线框导线的总电阻为R。则线框离开磁场的过程中( )
D．ad间的电压为
