题目内容
18．质量为3.0千克的物体A静止在水平桌面上．另一个质量为1.0千克的物体B以10.0米/秒的水平速度与物体A相撞，碰撞后物体B以2.0米/秒的速度反向弹回．相撞过程中损失的机械能是24焦．分析 碰撞过程中动量守恒，由动量守恒定律可以求出A的速度，由能量守恒定律可以求出损失的机械能．
解答 解：AB组成的系统动量守恒，以B的初速度方向为正方向，由动量守恒定律得：
mBvB=mBv′B+mAvA
即：1×10=1×（-2）+3×vA
解得：vA=4m/s，速度方向与正方向相同．
由能量守恒定律得：碰撞过程中损失的机械能
△E=$\frac{1}{2}$mBvB2-$\frac{1}{2}$mAvA2-$\frac{1}{2}$mBv′B2
解得：△E=24J；
故答案为：24．
点评 熟练应用动量守恒定律与能量守恒定律即可正确解题，应用动量守恒定律解题时，注意正方向的选择．
练习册系列答案
相关题目
据英国《每日邮报》报道，英式触式橄榄球球员赫普顿斯托尔（James Heptonstall）在伦敦成功挑战地铁速度．他从站点“Mansion House”下车，在下一地铁站点“Cannon Street”顺利登上刚下来的同一节车厢．已知地铁列车每次停站时间（从车门打开到关闭的时间）为ta=20s，列车加速和减速阶段的加速度均为a=1m/s2，运行过程的最大速度为vm=72km/h．假设列车运行过程中只做匀变速和匀速运动，两站之间的地铁轨道和地面道路都是平直的且长度相同，两站间的距离约为x=400m，赫普顿斯托尔出站和进站共用时tb=30s．问：
6．如图所示电路中，当开关S闭合时，电流表和电压表读数的变化是（ ）
| A． | 两表读数均变大 | B． | 电流表读数增大，电压表读数减小 | ||
| C． | 两表读数均变小 | D． | 电流表读数减小，电压表读数增大 |
13．
如图所示，质量为m的物块（视为质点），带正电Q，开始时让它静止在倾角α=60度的固定光滑绝缘斜面顶端，整个装置放在水平方向、大小为E=$\frac{\sqrt{3}mg}{Q}$的匀强电场中（设斜面顶端处电势为零），斜面高为H．释放后，物块落地时的电势能为?，物块落地时的速度大小v，则（ ）
如图所示，质量为m的物块（视为质点），带正电Q，开始时让它静止在倾角α=60度的固定光滑绝缘斜面顶端，整个装置放在水平方向、大小为E=$\frac{\sqrt{3}mg}{Q}$的匀强电场中（设斜面顶端处电势为零），斜面高为H．释放后，物块落地时的电势能为?，物块落地时的速度大小v，则（ ）| A． | Ep=-$\frac{\sqrt{3}}{3}$mgH | B． | ?=mgH | C． | v=2$\sqrt{gH}$ | D． | v=2gH |
3．2011年9月17日，国际田联钻石联赛布鲁赛尔站，约翰•布莱克以19秒26的恐怖成绩获得男子200米金牌，只比“闪电”博尔特名下的现世界纪录慢0.07秒．布莱克在比赛中，先做加速运动，然后匀速运动，最后加速冲刺．已知他的脚与地面间不会发生相对滑动，以下说法正确的是（ ）
| A． | 加速阶段地面对他的摩擦力做正功 | |
| B． | 匀速阶段地面对他的摩擦力做负功 | |
| C． | 由于他的脚与地面间不发生相对滑动，所以不论加速还是匀速，地面对他的摩擦力始终不对他做功 | |
| D． | 无论加速还是匀速阶段，地面对他的摩擦力始终做负功 |
10．线圈在磁场中匀速转动产生的交流电动势为e=10$\sqrt{2}$sin20πt （V），则下列说法中正确的是（ ）
| A． | t=0时，线圈平面位于中性面 | |
| B． | t=$\frac{1}{80}s$时，线圈的感应电动势为零 | |
| C． | t=$\frac{1}{40}s$时，导线切割磁感线的有效速度最大 | |
| D． | t=0.4 s时，e达峰值10$\sqrt{2}$ V |
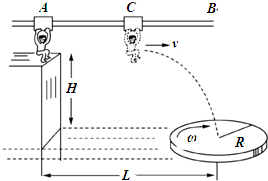某电视台“快乐向前冲”节目中的场地设施如题图所示，AB为水平直轨道，上面安装有电动悬挂器，可以载人运动，水面上漂浮着一个半径为R，角速度为ω，铺有海绵垫的转盘，转盘的轴心离平台的水平距离为L，平台边缘与转盘平面的高度差为H．选手抓住悬挂器，可以在电动机带动下，从A点下方的平台边缘处沿水平方向做初速度为零，加速度为a的匀加速直线运动．选手必须作好判断，在合适的位置释放，才能顺利落在转盘上．设人的质量为m（不计身高大小），人与转盘间的最大静摩擦力为μmg，重力加速度为g．
一根长为L的细绳，一端拴在水平轴O上，另一端有一个质量为m的小球．现使细绳位于水平位置并且绷紧，如图所示．给小球一个瞬间的作用，使它得到一定的向下的初速度