题目内容
传送带在工农业生产中有着广泛的应用．如图所示，平台上的人欲通过一根平行于传送带的轻绳将物品拉上平台，已知物品质量m=50kg，可看成质点，用F=500N的恒力从静止开始往上拉，传送带与水平面的夹角θ=37°，从传送带底端到平台左边的距离L=2.25m，传送带以恒定速度v=2m/s顺时针运行，物品与传送带之间的动摩擦因数μ=0.5，设最大静摩擦力等于滑动摩擦力．（g取10m/s2，sin 37°=0.6，cos 37°=0.8）问：（1）物品从传送带底端运动到平台上所用的时间是多少？
（2）若在物品离传送带底端L0=0.44m处时，立即撤去恒力F，求物品再经过多少时间离开传送带？
分析：（1）对物品进行受力分析，求出合外力，再根据牛顿第二定律求加速度，注意需要根据物品与传送带间速度大小判定滑动摩擦力的方向；
（2）判定产生位移0.44m时物品的速度，根据速度情况判断物品的运动情况，由运动情况确定运动时间．
（2）判定产生位移0.44m时物品的速度，根据速度情况判断物品的运动情况，由运动情况确定运动时间．
解答：解：（1）物品在达到传送带速度之前，由受力情况，据牛顿定律有：F+μmgcos37°-mgsin37°=ma1
解得：a1=8m/s2
由v=at 和x=
at2得：
t1=0.25s，x1=0.25m
随后由受力情况，据牛顿第二定律有：F-μmgcos37°-mgsin37°=ma2
解得：a1=0，即物品随传送带匀速上升
位移：x2=L-x1=2m，t2=
=1s
总时间：t=t1+t2=1.25s
（2）L0=0.44m＞x1=0.25m，物品的速度等于传送带的速度v=2m/s
撤去外力F，由物品受力情况，牛顿定律有：μmgcos37°-mgsin37°=ma3
代入数据解得：a3=-2m/s2
由 2ax=
-
代入数据解得：X3=1m
因为L0+x3=1.44m＜L=2.25m 物品速度减为零后倒回传送带底部，
由 x=v0t+
at2
代入数据解得：t3=2.2s
答：（1）物品从传送带底端运动到平台上所用的时间是1.25s
（2）若在物品离传送带底端L0=0.44m处时，立即撤去恒力F，物品再经过2.2s离开传送带．
解得：a1=8m/s2
由v=at 和x=
| 1 |
| 2 |
t1=0.25s，x1=0.25m
随后由受力情况，据牛顿第二定律有：F-μmgcos37°-mgsin37°=ma2
解得：a1=0，即物品随传送带匀速上升
位移：x2=L-x1=2m，t2=
| x2 |
| v |
总时间：t=t1+t2=1.25s
（2）L0=0.44m＞x1=0.25m，物品的速度等于传送带的速度v=2m/s
撤去外力F，由物品受力情况，牛顿定律有：μmgcos37°-mgsin37°=ma3
代入数据解得：a3=-2m/s2
由 2ax=
| v | 2 t |
| v | 2 0 |
代入数据解得：X3=1m
因为L0+x3=1.44m＜L=2.25m 物品速度减为零后倒回传送带底部，
由 x=v0t+
| 1 |
| 2 |
代入数据解得：t3=2.2s
答：（1）物品从传送带底端运动到平台上所用的时间是1.25s
（2）若在物品离传送带底端L0=0.44m处时，立即撤去恒力F，物品再经过2.2s离开传送带．
点评：本题关键是受力分析后，根据牛顿第二定律求解出加速度，然后根据运动学公式列式求解．
练习册系列答案
相关题目
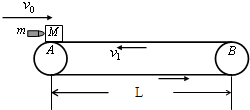传送带在工农业生产和日常生活中都有广泛的应用，例如在港口用传送带中运输货物，在机场上用传送带将地面上的行李传送到飞机上等．现有一个水平传送带装置AB，如右图所示．传送带的长度L=1m，质量M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动（传送带移动的速率始终恒定），木块与传送带间动摩擦因数μ=0.5．当木块运动到传送带最左端A点时，一颗质量为m=20g的子弹以v0=300m/s水平向右迎面射向木块并从木块中穿出，穿出时速度为u=50m/s．设子弹穿出木块的时间极短，且穿出木块以后子弹未与传送带作用．（传送带装置由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦，g=10m/s2）
传送带在工农业生产中有着广泛的应用．如图所示，平台上的人欲通过一根平行于传送带的轻绳将物品拉上平台，已知物品质量m=50kg，可看成质点，用F=500N的恒力从静止开始往上拉，传送带与水平面的夹角θ=37°，从传送带底端到平台左边的距离L=2.25m，传送带以恒定速度v=2m/s顺时针运行，物品与传送带之间的动摩擦因数μ=0.5，设最大静摩擦力等于滑动摩擦力．（g取10m/s2，sin 37°=0.6，cos 37°=0.8）问：
