题目内容
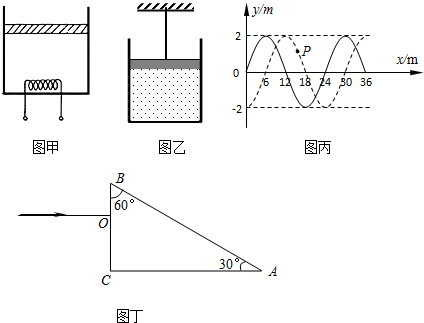
如图甲所示,光滑的水平地面上固定一长为L=1.7m长木板C,板的左端有两小物块A和B,其间夹有一根长为l=1.0m的轻弹簧,弹簧没有形变,且与物块不相连.已知mA=mC=20kg,mB=40kg,A与木板C、B与木板C的动摩擦因数分别为μA=0.50,μB=0.25,用水平力F作用于A,让F从零逐渐增大,并使B缓慢地向右移动了0.5m.问:

(1)若弹簧的劲度系数为k=200N/m,当B缓慢移动时,A、B物块之间的距离多大?
(2)若弹簧的劲度系数为k=200N/m,以作用力F为纵坐标,A移动的距离为横坐标,试在图乙的坐标系中作出推力F随A位移的变化图线.(直接作图,不必写出推导过程)
(3)当物块B缓慢地向右移动了0.5m时,撤去F,保持A、B两物块间距,将其间夹有的弹簧更换为压缩量仍相同、贮存的弹性势能为E=300J的新弹簧,并且同时释放三物体A、B和C,已被压缩的轻弹簧将A、B向两边弹开,哪一物块将先弹出木板C,最终C的速度是多少?

(1)若弹簧的劲度系数为k=200N/m,当B缓慢移动时,A、B物块之间的距离多大?
(2)若弹簧的劲度系数为k=200N/m,以作用力F为纵坐标,A移动的距离为横坐标,试在图乙的坐标系中作出推力F随A位移的变化图线.(直接作图,不必写出推导过程)
(3)当物块B缓慢地向右移动了0.5m时,撤去F,保持A、B两物块间距,将其间夹有的弹簧更换为压缩量仍相同、贮存的弹性势能为E=300J的新弹簧,并且同时释放三物体A、B和C,已被压缩的轻弹簧将A、B向两边弹开,哪一物块将先弹出木板C,最终C的速度是多少?
分析:先求出A与C间的摩擦力为fA=μAmAg=100N,B与C间摩擦力为fB=μBmBg=100N.力F从零逐渐增大,当增大到100N时,物块A开始向右移动压缩轻弹簧,此时B仍保持静止,弹簧的压缩量设为x,力F=fA+kx,当x=0.5m时,力F=fA+fB=200N,此时B将缓慢地向右移.B在移动0.5m的过程中,力F保持F=200N不变,弹簧压缩了0.5m,B离木板C的右端0.2m,A离木板C有左端1.0m.根据这些条件可作出力F随A位移的变化图线;
分析三个物体的运动状态:撤去力F之后,AB两物块给木板C的摩擦力的合力为零,木板静止不动,由动量守恒可求出AB速度之比,则可得到位移关系,判断哪个物块先
先弹出木板C.对三个物体,由能量守恒定律和动量守恒结合求解最终C的速度.
分析三个物体的运动状态:撤去力F之后,AB两物块给木板C的摩擦力的合力为零,木板静止不动,由动量守恒可求出AB速度之比,则可得到位移关系,判断哪个物块先
先弹出木板C.对三个物体,由能量守恒定律和动量守恒结合求解最终C的速度.
解答:解:(1)当B缓慢移动时,对B由平衡条件得:kx=μBmBg,解得:x=0.5m
则A、B物块之间的距离为SAB=l-x=0.5m
(2)A与C间的摩擦力为:fA=μAmAg=0.5×20×10N=100N,B与C间摩擦力为:fB=μBmBg=0.25×40×10N=100N,
推力F 从零逐渐增大,当增大到100N时,物块A开始向右移动压缩轻弹簧(此时B仍保持静止),设压缩量为x,
则力F=fA+kx,当x=0.5m时,力F=fA+fB=200N,此时B将缓慢地向右移.B在移动0.5m的过程中,力F保持F=200N不变,弹簧压缩了0.5m,
B离木板C的右端0.2m,A离木板C有左端1.0m.作出力F随A位移的变化图线如右图所示.
(3)撤去力F之后,A、B两物块给木板C的摩擦力的合力为零,故在物块A、B滑离木板C之前,C仍静止不动.物块A、B整体所受外力的合力也为零,其动量守恒,
可得:mAvA=mBvB…①
始终有vA:vB=mB:mA=2:1,
当物块B在木板C上向右滑动了0.2m,物块A则向左滑动了0.4m,但A离木板C的左端还有d=0.6m.
可见,物块B先滑离木板C.
并且两物块的相对位移△s=0.4+0.2m=0.6m>0.5m(弹簧的压缩量),弹簧贮存的弹性势能已全部释放,
由能量守恒定律有:E=
mA
+
mB
+f×△s…②
由②式求出物块B滑离木板C的A物块的速度:vA=4m/s
设此后A滑离木板C时,物块A的速度为v'A,木板C的速度为v'C,由动量守恒有:mAvA=mAv'A+mCv'C…③
由能量守恒有:fA×d=
mA
-(
mAv
+
mCv
)…④
将d=0.6m及有关数据代入③④两式可得:v
-4v′C+3=0
解得:v'C=1m/s(v'C=3m/s舍去)
答:(1)若弹簧的劲度系数为k=200N/m,当B缓慢移动时,A、B物块之间的距离0.5m
(2)如图
(3)当物块B缓慢地向右移动了0.5m时,撤去F最终C的速度是1m/s.
则A、B物块之间的距离为SAB=l-x=0.5m
(2)A与C间的摩擦力为:fA=μAmAg=0.5×20×10N=100N,B与C间摩擦力为:fB=μBmBg=0.25×40×10N=100N,
推力F 从零逐渐增大,当增大到100N时,物块A开始向右移动压缩轻弹簧(此时B仍保持静止),设压缩量为x,
则力F=fA+kx,当x=0.5m时,力F=fA+fB=200N,此时B将缓慢地向右移.B在移动0.5m的过程中,力F保持F=200N不变,弹簧压缩了0.5m,
B离木板C的右端0.2m,A离木板C有左端1.0m.作出力F随A位移的变化图线如右图所示.

(3)撤去力F之后,A、B两物块给木板C的摩擦力的合力为零,故在物块A、B滑离木板C之前,C仍静止不动.物块A、B整体所受外力的合力也为零,其动量守恒,
可得:mAvA=mBvB…①
始终有vA:vB=mB:mA=2:1,
当物块B在木板C上向右滑动了0.2m,物块A则向左滑动了0.4m,但A离木板C的左端还有d=0.6m.
可见,物块B先滑离木板C.
并且两物块的相对位移△s=0.4+0.2m=0.6m>0.5m(弹簧的压缩量),弹簧贮存的弹性势能已全部释放,
由能量守恒定律有:E=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
由②式求出物块B滑离木板C的A物块的速度:vA=4m/s
设此后A滑离木板C时,物块A的速度为v'A,木板C的速度为v'C,由动量守恒有:mAvA=mAv'A+mCv'C…③
由能量守恒有:fA×d=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| ′ | 2 A |
| 1 |
| 2 |
| ′ | 2 C |
将d=0.6m及有关数据代入③④两式可得:v
| ′ | 2 C |
解得:v'C=1m/s(v'C=3m/s舍去)
答:(1)若弹簧的劲度系数为k=200N/m,当B缓慢移动时,A、B物块之间的距离0.5m
(2)如图
(3)当物块B缓慢地向右移动了0.5m时,撤去F最终C的速度是1m/s.
点评:本题难度较大,既要分析三个物体的受力情况,确定出它们的运动状态,还要根据动量守恒和能量守恒定律结合求解C的最终速度.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目