题目内容
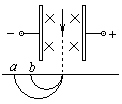
如图所示,一带电粒子以某一速度在竖直平面内做直线运动,经过一段时间后进入一垂直于纸面向里、磁感应强度为B的最小的圆形匀强磁场区域(图中未画出磁场区域),粒子飞出磁场后垂直电场方向进入宽为L的匀强电场。电场强度大小为E,方向竖直向上。当粒子穿出电场时速度大小变为原来的 倍。已知带电粒子的质量为m,电量为g,重力不计。粒子进入磁场前的速度如图与水平方向成θ=60°角。求:
倍。已知带电粒子的质量为m,电量为g,重力不计。粒子进入磁场前的速度如图与水平方向成θ=60°角。求:

(1)粒子带什么性质的电荷;
(2)粒子在磁场中运动时速度多大;
(3)该最小的圆形磁场区域的面积为多大?
 倍。已知带电粒子的质量为m,电量为g,重力不计。粒子进入磁场前的速度如图与水平方向成θ=60°角。求:
倍。已知带电粒子的质量为m,电量为g,重力不计。粒子进入磁场前的速度如图与水平方向成θ=60°角。求:
(1)粒子带什么性质的电荷;
(2)粒子在磁场中运动时速度多大;
(3)该最小的圆形磁场区域的面积为多大?
(1)负电;(2)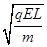 (3)
(3)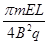
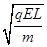 (3)
(3)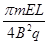
试题分析:(1)根据粒子在磁场中偏转的情况和左手定则可知,粒子带负电。
(2)由于洛伦兹力对粒子不做功,故粒子以原来的速率进入电场中,设带电粒子进入电场的初速度为v0,在电场中偏转时做类平抛运动,由题意知粒子离开电场时的末速度大小为
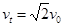 ,将
,将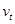 分解为平行于电场方向和垂直于电场方向的两个分速度
分解为平行于电场方向和垂直于电场方向的两个分速度由几何关系知
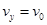 ①
① 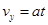 ②
② 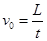 ③
③ 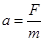 ④
④ 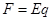 ⑤
⑤ 联立求解①②③④⑤得
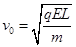
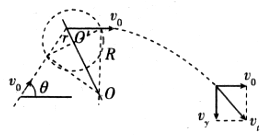
(3)如图所示,带电粒子在磁场中所受洛伦兹力作为向心力,设在磁场中做圆周运动的半径为R,圆形磁场区域的半径为r,则
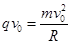 ⑦
⑦ 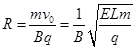 ⑧
⑧ 由几何知识可得:r=Rsin30° ⑨
磁场区域的最小面积为
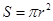 ⑩
⑩ 联立求解⑧⑨⑩得
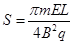

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目


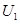 ;极板M、N长为L,间距为
;极板M、N长为L,间距为 ,也板间电压为
,也板间电压为 ,磁场的磁感应强度大小为B、方向垂直纸面向里,磁场的左边界与中心轴线垂直.不计粒子的重力及其相互间的作用.求
,磁场的磁感应强度大小为B、方向垂直纸面向里,磁场的左边界与中心轴线垂直.不计粒子的重力及其相互间的作用.求
 的正切值;
的正切值;
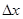


 ,由此可知,打在两点的粒子质量差上
,由此可知,打在两点的粒子质量差上 =___ _(均带电量为q的正电荷)。
=___ _(均带电量为q的正电荷)。