题目内容
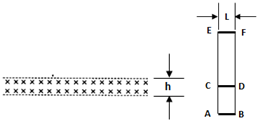
如图所示,水平方向有界匀强磁场的高度h=1m、磁感应强度B=
T.竖直放置的“日”字型闭合导体线框ABFE,宽L=1m,质量m=0.25kg,AC、CE的长度都大于h,AB边的电阻RAB=1Ω、CD边的电阻RCD=2Ω、EF边的电阻REF=3Ω,其余电阻不计.线框由静止下落,AB边进入磁场时恰能匀速运动,不计空气阻力,g取10m/s2.求:
(1)开始下落时,线框AB边离磁场上边界的高度h1为多少?
(2)若线框CD边刚进入磁场时也做匀速运动,AB边与CD边的距离h2为多少?
(3)在满足(1)(2)前提下,若线框EF边刚进磁场时也做匀速运动,则从开始下落到EF边离开磁场过程中,线框中产生的焦耳热Q为多少?
| ||
| 4 |
(1)开始下落时,线框AB边离磁场上边界的高度h1为多少?
(2)若线框CD边刚进入磁场时也做匀速运动,AB边与CD边的距离h2为多少?
(3)在满足(1)(2)前提下,若线框EF边刚进磁场时也做匀速运动,则从开始下落到EF边离开磁场过程中,线框中产生的焦耳热Q为多少?

分析:(1)AB边进入磁场时切割磁感线,产生感应电动势相当于电源,CD与EF并联.由于线框匀速运动,重力与安培力平衡,根据平衡条件求出线框的速度,线框示进入磁场时做自由落体运动,由h1=
求出h1.
(2)若线框CD边刚进入磁场时做匀速运动,重力与安培力平衡,由平衡条件求出此时线框的速度v2,AB出出磁场到CD进磁场,穿过线框的磁通量不变,没有感应电流产生,线框做加速度为g的匀加速运动,由运动学公式求解h2.
(3)线框EF边刚进磁场时也做匀速运动,重力与安培力也平衡,由平衡条件求出此时线框的速度v3,由运动学公式求出CE高度HCE.
| ||
| 2g |
(2)若线框CD边刚进入磁场时做匀速运动,重力与安培力平衡,由平衡条件求出此时线框的速度v2,AB出出磁场到CD进磁场,穿过线框的磁通量不变,没有感应电流产生,线框做加速度为g的匀加速运动,由运动学公式求解h2.
(3)线框EF边刚进磁场时也做匀速运动,重力与安培力也平衡,由平衡条件求出此时线框的速度v3,由运动学公式求出CE高度HCE.
解答:解:(1)AB边匀速进磁场,设速度为v1.
mg=F安=BI1L=
得,v1=
=8m/s
h1=
=
m=3.2m
(2)CD边匀速进磁场,设速度为v2.
mg=F安=BI2L=
v2=
=10m/s
则h2=
+h=2.8m
(3)EF边匀速进磁场,设速度为v3.
mg=F安=BI3L=
v3=
=
m/s
HCE=
+h=
m
Q=mg(h1+h+HAC+HCE)-
m
=7.5J
答:(1)开始下落时,线框AB边离磁场上边界的高度h1为3.2m.
(2)AB边与CD边的距离h2为2.8m.
(3)从开始下落到EF边离开磁场过程中,线框中产生的焦耳热Q为7.5J.
mg=F安=BI1L=
| B2L2v1 |
| R1 |
得,v1=
mg(RAB+
| ||
| B2L2 |
h1=
| ||
| 2g |
| 82 |
| 2×10 |
(2)CD边匀速进磁场,设速度为v2.
mg=F安=BI2L=
| B2L2v2 |
| R2 |
v2=
mg(RCD+
| ||
| B2L2 |
则h2=
| ||||
| 2g |
(3)EF边匀速进磁场,设速度为v3.
mg=F安=BI3L=
| B2L2v3 |
| R3 |
v3=
mg(REF+
| ||
| B2L2 |
| 40 |
| 3 |
HCE=
| ||||
| 2g |
| 44 |
| 9 |
Q=mg(h1+h+HAC+HCE)-
| 1 |
| 2 |
| v | 2 3 |
答:(1)开始下落时,线框AB边离磁场上边界的高度h1为3.2m.
(2)AB边与CD边的距离h2为2.8m.
(3)从开始下落到EF边离开磁场过程中,线框中产生的焦耳热Q为7.5J.
点评:本题是电磁感应与电路、力学、磁场等知识的综合应用,关键有三点:一是认识电路的结构;二是计算安培力;三是分析能量是如何转化的.第(3)问也可以这样求解:只有AB边、CD边、EF边在磁场中运动时,线框中才产生热量,现在三个边在磁场中均做匀速运动,所以Q=3mgh=3×0.25×10×1J=7.5J.

练习册系列答案
相关题目
 T。竖直放置的“日”字型闭合导体线框ABFE,宽L=1m,质量m=0.25kg,AC、CE的长度都大于h,AB边的电阻RAB=1Ω、CD边的电阻RCD=2Ω、EF边的电阻REF=3Ω,其余电阻不计。线框由静止下落,AB边进入磁场时恰能匀速运动,不计空气阻力,g取10m/s2。求:
T。竖直放置的“日”字型闭合导体线框ABFE,宽L=1m,质量m=0.25kg,AC、CE的长度都大于h,AB边的电阻RAB=1Ω、CD边的电阻RCD=2Ω、EF边的电阻REF=3Ω,其余电阻不计。线框由静止下落,AB边进入磁场时恰能匀速运动,不计空气阻力,g取10m/s2。求:

 (1)导线所受安培力有多大?方向如何?
(1)导线所受安培力有多大?方向如何?