题目内容
如图所示,物体重30N,用绳悬挂在O点,OC绳能承受的最大拉力为20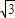 N,再用一绳系在OC绳的A点,BA绳能承受的最大拉力为30N.现用水平拉BA,则可以把OA绳拉到与竖直方向成( )
N,再用一绳系在OC绳的A点,BA绳能承受的最大拉力为30N.现用水平拉BA,则可以把OA绳拉到与竖直方向成( )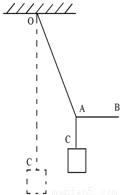
A.30°
B.大于30°小于45°
C.45°
D.60°
【答案】分析:在拉动的过程中,为了保证绳不拉断,先判断出那根绳先断,用这根绳刚要断时的拉力做为临界条件分析计算.
解答:解:当OA绳与竖直方向的夹角θ逐渐增大时,OA和BA绳中的拉力都逐渐增大.当其中某一根的拉力达到它本身能承受的最大拉力时,就不能再增大角度了.
结点A的受力如图所示.
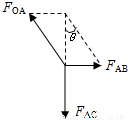
由图可知,
OA绳的拉力总是大于AB绳的拉力,且绳所能承受的最大拉力又比AB绳的小.
因此,OA绳的拉力先达到断裂的临界值,应用OA的承受的最大拉力作为临界条件求解.
此时:FOA =20 N
N
FAC=G=30N
则cosθ=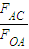 =
=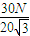 =
=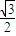
故OA偏离竖直方向的最大角度θ=30°
故选A
点评:此题是物体受力平衡的应用,解决此类题目需要找出临界状态,再应用受力平衡计算即可.
解答:解:当OA绳与竖直方向的夹角θ逐渐增大时,OA和BA绳中的拉力都逐渐增大.当其中某一根的拉力达到它本身能承受的最大拉力时,就不能再增大角度了.
结点A的受力如图所示.

由图可知,
OA绳的拉力总是大于AB绳的拉力,且绳所能承受的最大拉力又比AB绳的小.
因此,OA绳的拉力先达到断裂的临界值,应用OA的承受的最大拉力作为临界条件求解.
此时:FOA =20
 N
N FAC=G=30N
则cosθ=
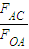 =
=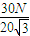 =
=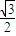
故OA偏离竖直方向的最大角度θ=30°
故选A
点评:此题是物体受力平衡的应用,解决此类题目需要找出临界状态,再应用受力平衡计算即可.

练习册系列答案
相关题目
如图所示,物体重30 N,用OC绳悬挂于O点,OC绳能承受的最大拉力为303 N.再用一绳系在OC绳上的A点,BA绳能承受的最大拉力为30 N.现用水平力拉BA,可以把OA绳拉到与竖直方向成多大角度?

 如图所示,物体重G=100N,并保持静止.绳子AC与BC分别与竖直方向成30°角和60°角,则绳子AC和BC的拉力分别为多大?
如图所示,物体重G=100N,并保持静止.绳子AC与BC分别与竖直方向成30°角和60°角,则绳子AC和BC的拉力分别为多大?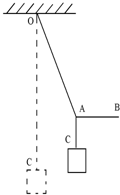 (2006?和平区模拟)如图所示,物体重30N,用绳悬挂在O点,OC绳能承受的最大拉力为20
(2006?和平区模拟)如图所示,物体重30N,用绳悬挂在O点,OC绳能承受的最大拉力为20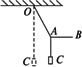
 N,再用一绳系在OC绳的A点,BA绳能承受的最大拉力为30 N,现用水平力拉BA绳,可以把OA绳拉到与竖直方向成多大角度?
N,再用一绳系在OC绳的A点,BA绳能承受的最大拉力为30 N,现用水平力拉BA绳,可以把OA绳拉到与竖直方向成多大角度? 