题目内容
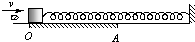 如图,一轻质弹簧一端固定、另一端与质量为M的小滑块连接,开始时滑块静止在水平导轨的O点,弹簧处于原长状态.导轨的OA段是粗糙的,其余部分都是光滑的.有一质量为m的子弹以大小为v的速度水平向右射入滑块,并很快停留在滑块中.之后,滑块先向右滑行并越过A点,然后再向左滑行,最后恰好停在出发点O处.
如图,一轻质弹簧一端固定、另一端与质量为M的小滑块连接,开始时滑块静止在水平导轨的O点,弹簧处于原长状态.导轨的OA段是粗糙的,其余部分都是光滑的.有一质量为m的子弹以大小为v的速度水平向右射入滑块,并很快停留在滑块中.之后,滑块先向右滑行并越过A点,然后再向左滑行,最后恰好停在出发点O处.(1)求滑块滑行过程中弹簧弹性势能的最大值.
(2)滑块停在O点后,另一质量也为m的子弹以另一速度水平向右射入滑块并很快停留在滑块中,此后滑块滑行过程先后有两次经过O点.求第二颗子弹入射前的速度u的大小在什么范围内?
分析:(1)一颗子弹射入滑块后,根据动量守恒定律求出速度.滑块向右滑行至最右端时,弹簧弹性势能达到最大,由能量守恒定律列出方程.滑块由最右端向左滑行至O点,再由功能关系得到弹簧的弹性势能与OA段的长度的关系式,联立求出弹簧弹性势能的最大值.
(2)由动量守恒定律求出第二颗子弹射入滑块后滑块的速度,若滑块第一次返回O点时就停下,根据能量守恒定律求出速度u;若滑块第一次返回O点后继续向左滑行,再向右滑行,且重复第一次滑行过程,最后停在O点,由能量守恒定律求出速度u,联立即可得到速度u的范围.
(2)由动量守恒定律求出第二颗子弹射入滑块后滑块的速度,若滑块第一次返回O点时就停下,根据能量守恒定律求出速度u;若滑块第一次返回O点后继续向左滑行,再向右滑行,且重复第一次滑行过程,最后停在O点,由能量守恒定律求出速度u,联立即可得到速度u的范围.
解答:解:(1)设OA段的长度为l,与滑块间的动摩擦因数为μ.
设第一颗子弹射入滑块后滑块的速度为v1,由动量守恒定律得:mv=(M+m)v1 …①
滑块向右滑行至最右端时,弹簧弹性势能达到最大,设为EP,由功能关系得:
(M+m)
=μ(M+m)gl+EP…②
滑块由最右端向左滑行至O点,由功能关系得:EP=μ(M+m)gl…③
解得:EP=
…④
②设第二颗子弹射入滑块后滑块的速度为v2,由动量守恒定律得:mu=(M+2m)v2 …⑤.
若滑块第一次返回O点时就停下,则滑块的运动情况与前面的情况相同:
(M+2m)
=μ(M+2m)g?2l…⑥
解得u=
v…⑦
若滑块第一次返回O点后继续向左滑行,再向右滑行,且重复第一次滑行过程,最后停在O点,则
(M+2m)
=μ(M+2m)g?4l…⑧
解得:u=
v…⑨
第二颗子弹入射前的速度u的大小在以下范围内
v<u<
v
答:(1)滑块滑行过程中弹簧弹性势能的最大值为
.
(2)第二颗子弹入射前的速度u的大小在以下范围内
v<u<
v.
设第一颗子弹射入滑块后滑块的速度为v1,由动量守恒定律得:mv=(M+m)v1 …①
滑块向右滑行至最右端时,弹簧弹性势能达到最大,设为EP,由功能关系得:
| 1 |
| 2 |
| v | 2 1 |
滑块由最右端向左滑行至O点,由功能关系得:EP=μ(M+m)gl…③
解得:EP=
| m2v2 |
| 4(M+m) |
②设第二颗子弹射入滑块后滑块的速度为v2,由动量守恒定律得:mu=(M+2m)v2 …⑤.
若滑块第一次返回O点时就停下,则滑块的运动情况与前面的情况相同:
| 1 |
| 2 |
| v | 2 2 |
解得u=
| M+2m |
| M+m |
若滑块第一次返回O点后继续向左滑行,再向右滑行,且重复第一次滑行过程,最后停在O点,则
| 1 |
| 2 |
| v | 2 2 |
解得:u=
| M+2m |
| M+m |
| 2 |
第二颗子弹入射前的速度u的大小在以下范围内
| M+2m |
| M+m |
| M+2m |
| M+m |
| 2 |
答:(1)滑块滑行过程中弹簧弹性势能的最大值为
| m2v2 |
| 4(M+m) |
(2)第二颗子弹入射前的速度u的大小在以下范围内
| M+2m |
| M+m |
| M+2m |
| M+m |
| 2 |
点评:本题是动量守恒和能量守恒的综合,要挖掘隐含的临界条件,确定速度u的速度范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,在同一竖直平面内,一轻质弹簧一端固定,另一自由端恰好与水平线AB齐平,静止放于光滑斜面上,一长为L的轻质细线一端固定在O点,另一端系一质量为m的小球,将细线拉至水平,此时小球在位置C,由静止释放小球,小球到达最低点D时,细绳刚好被拉断,D点到AB的距离为h,之后小球在运动过程中恰好沿斜面方向将弹簧压缩,弹簧的最大压缩量为x,重力加速度为g.求:
如图所示,在同一竖直平面内,一轻质弹簧一端固定,另一自由端恰好与水平线AB齐平,静止放于光滑斜面上,一长为L的轻质细线一端固定在O点,另一端系一质量为m的小球,将细线拉至水平,此时小球在位置C,由静止释放小球,小球到达最低点D时,细绳刚好被拉断,D点到AB的距离为h,之后小球在运动过程中恰好沿斜面方向将弹簧压缩,弹簧的最大压缩量为x,重力加速度为g.求: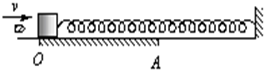 物理--选修3-5
物理--选修3-5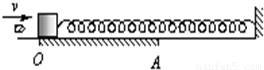
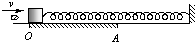 如图,一轻质弹簧一端固定、另一端与质量为M的小滑块连接,开始时滑块静止在水平导轨的O点,弹簧处于原长状态.导轨的OA段是粗糙的,其余部分都是光滑的.有一质量为m的子弹以大小为v的速度水平向右射入滑块,并很快停留在滑块中.之后,滑块先向右滑行并越过A点,然后再向左滑行,最后恰好停在出发点O处.
如图,一轻质弹簧一端固定、另一端与质量为M的小滑块连接,开始时滑块静止在水平导轨的O点,弹簧处于原长状态.导轨的OA段是粗糙的,其余部分都是光滑的.有一质量为m的子弹以大小为v的速度水平向右射入滑块,并很快停留在滑块中.之后,滑块先向右滑行并越过A点,然后再向左滑行,最后恰好停在出发点O处.