题目内容
在平静的水面上，有一条载人的小船，船的质量为M，人的质量为m，人相对船静止，船和人以速度v0前进.（1）当人相对船以速度u沿跟船的运动相反方向行走时，船的速度多大？（2）若船长为L，且开始时系统静止，当人从船的一头走到另一头停止时，船后退的距离是多少？（水的阻力不计）
解析：本题考查动量守恒定律，以及动量的相对性，解答时分清作用前后各物体动量，然后应用动量守恒定律即可.同时还应注意此类题的解题步骤.
①应该把人对船的速度变为人对地的速度，即各物体的运动应对同一参考系.
②人走船也走，人停船也停，因此整个过程系统动量变化为零，人在船上不管做什么运动船后退的距离一定相同.
③人船模型可以推广到“人车模型”和“子弹打木块”模型，它们的解法类似.
（1）人和船组成系统，水平方向动量守恒，由于人对地速度为v-u，则由动量守恒定律知
（m+M）v0=Mv+m(v-u)
所以v=v0+
u，方向与v0方向相同.
（2）开始时人船都停止，总动量为零，设人在船上走一段较短时间Δt时，人和船都看作是匀速运动，推广到整个过程时，人的平均速度为
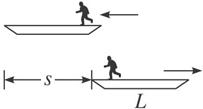
，船的平均速度为
，如下图.设船后退s，则人的位移为L-s，由动量守恒定律
m
-M
=0
，所以s=
.
答案：（1）v=v0+
u，方向与v0方向相同
（2）
练习册系列答案
名校课堂系列答案
相关题目
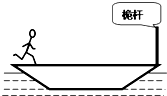某健身游戏过程可简化为如图所示物理模型．在平静的水面上，有一长L=12m的木船，木船右端固定一直立桅杆，木船和桅杆的总质量m1=200kg，质量为m2=50kg的人立于木船左端，开始时木船与人均静止，若人匀加速向右奔跑（没有打滑）到右端并立即抱住桅杆，经历的时间是t=2s，船运动中受到水的阻力是船（包括人）总重的0.1倍，g取10m/s2，求：从人起跑到抱住桅杆之前的过程中．