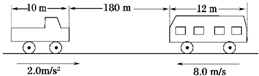
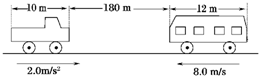
题目内容
一辆长为12m的客车沿平直公路以8.0m/s的速度匀速向北行驶,一辆长为17m的货车由静止开始以2.0m/s2的加速度由北向南匀加速行驶,已知货车刚启动时两车车头相距180m,求两车错车(即从车头相遇到车尾通过)所用的时间?
设货车启动后经过时间t1时两车开始错车,则有
x1=
a
x2=vt1
x1+x2=180m
联立解得:t1=10s
设货车从开始运动到两车错车结束所有时间表为t2,有
x1+x2′=(180+12+17)m=209m
x1′=
a
x2′=vt2
解得 t2=11s
故两车错车时间△t=t2-t1=1s
答:两车错车(即从车头相遇到车尾通过)所用的时间为1s
x1=
| 1 |
| 2 |
| t | 21 |
x2=vt1
x1+x2=180m
联立解得:t1=10s
设货车从开始运动到两车错车结束所有时间表为t2,有
x1+x2′=(180+12+17)m=209m
x1′=
| 1 |
| 2 |
| t | 22 |
x2′=vt2
解得 t2=11s
故两车错车时间△t=t2-t1=1s
答:两车错车(即从车头相遇到车尾通过)所用的时间为1s

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目