题目内容
【题目】如图所示，一轻弹簧原长L=1m，其一端固定在倾角为37°的固定直轨道AC的底端A处，另一端位于直轨道上B处，弹簧处于自然状态，AC＝3.5L。质量m=1kg的小物块P自C点由静止开始下滑，最低到达E点(未画出)，随后P沿轨道被弹回，最高到达F点，AF＝2L，已知P与直轨道间的动摩擦因数μ＝0.25。（取sin 37°＝0.6，cos 37°＝0.8，重力加速度g取10m/s2) 求：
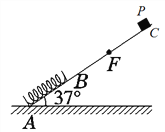
(1)P第一次运动到B点时速度的大小；
(2)P运动到E点时弹簧的压缩量x及弹簧的弹性势能EP。
【答案】（1）
（2）x=0.5m，EP=12J
【解析】(1)根据题意知，B、C之间的距离为3.5L-L=2.5L
设P到达B点时的速度为vB，由动能定理得
mg (2.5L)sin37°－μmg (2.5L)cos37°＝
解得vB＝2
m/s
(2)设BE＝x，P到达E点时弹簧的弹性势能为Ep，P由C点运动到E点再弹回到F点的过程中，由动能定理有
mg（3.5L-2L）sin37°－μmgL1cos37°＝0
且 L1=2.5L+2x+L
解得x=0.5m
P由C点运动到E点的过程中，由动能定理有
(mgsin37°－μmgcos37°)( 2.5L+x)-W弹＝0
则 Ep＝W弹＝12J
练习册系列答案
相关题目
