题目内容
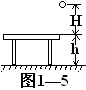
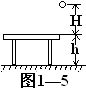
从离地h高处有静止释放一个质量为m的小球A,同时在它正下方的地面处以速度v0 竖直上抛另一个质量也为m的小球B.已知空气对小球的阻力f大小不变且f=
mg问:
(1)若h=15m,v0=20m/s 则经过多长时间小球B与A球相遇.
(2)若h=50m,v0=30m/s 则经过多长时间小球B与A相遇.
| 1 | 2 |
(1)若h=15m,v0=20m/s 则经过多长时间小球B与A球相遇.
(2)若h=50m,v0=30m/s 则经过多长时间小球B与A相遇.
分析:(1)由于是一个是下落,一个是上泡,先判定两物体是在上升阶段相遇还是在下降阶段相遇,由此在由位移之和等于高度来求时间.
(2)同第一问的方法,先判定两物体是在上升阶段相遇还是在下降阶段相遇,本题由于给了两个高度,所以据估计对高度大的这一问,物体应该在下降阶段相遇,验证可以得到具体结论,然后再据此来求相遇所需要的时间.
(2)同第一问的方法,先判定两物体是在上升阶段相遇还是在下降阶段相遇,本题由于给了两个高度,所以据估计对高度大的这一问,物体应该在下降阶段相遇,验证可以得到具体结论,然后再据此来求相遇所需要的时间.
解答:解:(1)B上升至最高点所需的时间:t1=
由牛顿第二定律:mg+
mg=ma1
解得:
a1=
g
t1=
s
此时间内,A的下降位移为:h1=
gt2=
m
B上升的位移为:
h2=
t=
m
h1+h2>15m
故应该是在B上升阶段相遇,设相遇时间为t,则由运动学可得:
?
gt2+v0t-
?
gt2=h
解得:t=1s t=-3s(舍弃)
(2)B上升至最高点所需的时间为:t2=
=2s
此过程B上升的高度为:s1=
=30m
此过程A下降的高度为:s2=
?
gt2=10m
上升和下降高度和为:s1+s2=40m
总高度为50m,故应是在B下降时相遇
在下降过程中A.B的加速度都是:
a=
=
g
设再经过t′的时间追上
A此时的速度:
vA=
gt2=10m/s
则:
vAt′+
?
gt′2+v0t-
?
gt′2=h-s1-s2
解得:t′=1s
所以相遇时间为:t=t2+t′=3s
答:
(1)若h=15m,v0=20m/s 则经过1s小球B与A球相遇.
(2)若h=50m,v0=30m/s 则经过3s小球B与A相遇.
| v0 |
| a1 |
由牛顿第二定律:mg+
| 1 |
| 2 |
解得:
a1=
| 3 |
| 2 |
t1=
| 4 |
| 3 |
此时间内,A的下降位移为:h1=
| 1 |
| 2 |
| 80 |
| 9 |
B上升的位移为:
h2=
| v0 |
| 2 |
| 40 |
| 3 |
h1+h2>15m
故应该是在B上升阶段相遇,设相遇时间为t,则由运动学可得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解得:t=1s t=-3s(舍弃)
(2)B上升至最高点所需的时间为:t2=
| v0 |
| a1 |
此过程B上升的高度为:s1=
| v02 |
| 2a1 |
此过程A下降的高度为:s2=
| 1 |
| 2 |
| 1 |
| 2 |
上升和下降高度和为:s1+s2=40m
总高度为50m,故应是在B下降时相遇
在下降过程中A.B的加速度都是:
a=
| mg-f |
| m |
| 1 |
| 2 |
设再经过t′的时间追上
A此时的速度:
vA=
| 1 |
| 2 |
则:
vAt′+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:t′=1s
所以相遇时间为:t=t2+t′=3s
答:
(1)若h=15m,v0=20m/s 则经过1s小球B与A球相遇.
(2)若h=50m,v0=30m/s 则经过3s小球B与A相遇.
点评:本题涉及的重要的内容是竖直上抛问题中的返回问题,和水平的直线相遇不同,竖直上抛不一定就是在上升阶段相遇,而极有可能在下降阶段相遇,尤其在出现两个高度的情况下,更应留意大的高度的相遇点的判定.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 mg问:
mg问: