题目内容
(10分)如图2所示,半径为r的绝缘细圆环的环面固定在水平面上,场强为E的匀强电场与环面平行。一电量为+q、质量为m的小球穿在环上,可沿环作无摩擦的圆周运动,若小球经A点时,速度vA的方向恰与电场垂直,且圆环与小球间沿水平方向无力的作用,试计算:

(1)小球运动达到最大速度的位置(半径与竖直方向成的角度θ用字母表示)
(2) 速度vA的大小;
(3)小球运动到与A点对称的B点时,对环在水平方向的作用力。

(1)小球运动达到最大速度的位置(半径与竖直方向成的角度θ用字母表示)
(2) 速度vA的大小;
(3)小球运动到与A点对称的B点时,对环在水平方向的作用力。
(1) 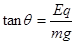 (2)
(2) (3)
(3) 。
。
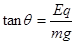 (2)
(2) (3)
(3) 。
。(1) 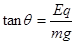
(2)在A点,小球在水平方向只受电场力作用,根据牛顿第二定律得:
 所以小球在A点的速度
所以小球在A点的速度 。
。
(3)在小球从A到B的过程中,根据动能定理,电场力做的正功等于小球动能的增加量,即 ,
,
小球在B点时,根据牛顿第二定律,在水平方向有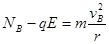
解以上两式,小球在B点对环的水平作用力为: 。
。
本题考查复合场和圆周运动、动能定理的综合应用,把重力和电场力进行合成,转化为等效重力场,在等效重力场的最低点小球速度最大,根据圆周运动沿着半径方向的合力提供向心力可求得在A点速度大小,从A到B运动过程中只有电场力做功,由动能定理求得B点速度,再由圆周运动的合力提供向心力求得环的支持力大小
点评:本题综合性比较强,考到的知识点很多,这就需要学生对圆周运动、动能定理、等效重力场的受力特点非常熟悉并能够加以应用
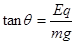
(2)在A点,小球在水平方向只受电场力作用,根据牛顿第二定律得:
 所以小球在A点的速度
所以小球在A点的速度 。
。(3)在小球从A到B的过程中,根据动能定理,电场力做的正功等于小球动能的增加量,即
 ,
,小球在B点时,根据牛顿第二定律,在水平方向有
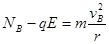
解以上两式,小球在B点对环的水平作用力为:
 。
。本题考查复合场和圆周运动、动能定理的综合应用,把重力和电场力进行合成,转化为等效重力场,在等效重力场的最低点小球速度最大,根据圆周运动沿着半径方向的合力提供向心力可求得在A点速度大小,从A到B运动过程中只有电场力做功,由动能定理求得B点速度,再由圆周运动的合力提供向心力求得环的支持力大小
点评:本题综合性比较强,考到的知识点很多,这就需要学生对圆周运动、动能定理、等效重力场的受力特点非常熟悉并能够加以应用

练习册系列答案
相关题目

 m/s
m/s  m/s
m/s

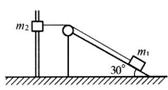
 m,又知当物体m2由图中位置(连接m2的轻绳此时水平)从静止开始下滑1m时,m1和m2受力恰好平衡。试求:(g取10 m/s2 )
m,又知当物体m2由图中位置(连接m2的轻绳此时水平)从静止开始下滑1m时,m1和m2受力恰好平衡。试求:(g取10 m/s2 )