题目内容
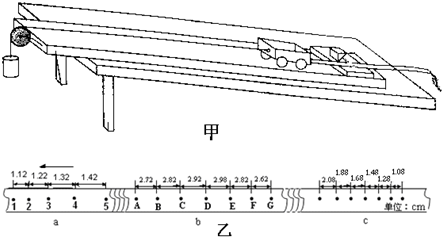
如图甲所示,小车放在斜面上,车前端栓有不可伸长的细线,跨过固定在斜面边缘的小滑轮与重物相连,小车后面与打点计时器的纸带相连.起初小车停在靠近打点计时器的位置,重物到地面的距离小于小车到滑轮的距离.启动打点计时器,释放重物,小车在重物的牵引下,由静止开始沿斜面向上运动,重物落地后,小车会继续向上运动一段距离.打点计时器使用的交流电频率为50Hz.图乙中a、b、c是小车运动时打下的纸带上的三段,纸带的运动方向如图乙中箭头所示.

(1)根据所提供纸带上的数据,可计算出打a段纸带时小车的加速度大小为______m/s2;打c段纸带时小车的加速度大小为______m/s2.(结果保留两位有效数字)
(2)请根据你计算的加速度情况,可判断出小车运动的最大速度可能出现在b段纸带中的______两点之间.
(3)如果重力加速度g取10m/s2,请你根据纸带上的数据推算出重物与小车的质量之比.

(1)根据所提供纸带上的数据,可计算出打a段纸带时小车的加速度大小为______m/s2;打c段纸带时小车的加速度大小为______m/s2.(结果保留两位有效数字)
(2)请根据你计算的加速度情况,可判断出小车运动的最大速度可能出现在b段纸带中的______两点之间.
(3)如果重力加速度g取10m/s2,请你根据纸带上的数据推算出重物与小车的质量之比.
(1)根据△x=aT2得:
a段纸带时小车的加速度aa=
=
=2.5m/s2
打c段纸带时小车的加速度ac=
=
=-5.0m/s2
所以打c段纸带时小车的加速度大小为5.0 m/s2.
(2)b段中只有DE之间位移最大,所以最大速度一定在DE之间.
(3)设小车的质量为M,重物的质量为m,斜面的倾角为θ,小车与斜面之间的滑动摩擦力Ff,小车加速过程中,
对小车和重物整体应用牛顿第二定律得mg-Mgsinθ-Ff=(M+m)a1
当重物落地后,小车减速上升的过程中应用牛顿第二定律得Mgsinθ+Ff=Ma2
联立两式并将a1=2.5m/s2和a2=5.0m/s2的数值代入得
=
故答案为:(1)2.5; 5.0;
(2)DE区间内;
(3)1;1
a段纸带时小车的加速度aa=
| △xa |
| T2 |
| 0.001 |
| 0.02×0.02 |
打c段纸带时小车的加速度ac=
| △xc |
| T2 |
| -0.002 |
| 0.02×0.02 |
所以打c段纸带时小车的加速度大小为5.0 m/s2.
(2)b段中只有DE之间位移最大,所以最大速度一定在DE之间.
(3)设小车的质量为M,重物的质量为m,斜面的倾角为θ,小车与斜面之间的滑动摩擦力Ff,小车加速过程中,
对小车和重物整体应用牛顿第二定律得mg-Mgsinθ-Ff=(M+m)a1
当重物落地后,小车减速上升的过程中应用牛顿第二定律得Mgsinθ+Ff=Ma2
联立两式并将a1=2.5m/s2和a2=5.0m/s2的数值代入得
| m |
| M |
| 1 |
| 1 |
故答案为:(1)2.5; 5.0;
(2)DE区间内;
(3)1;1

练习册系列答案
相关题目