题目内容
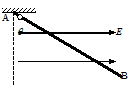
如图所示,一固定直杆AB长为L=2m,与竖直方向的夹角为q=53°,一质量为m=4kg、电荷量为q=+3´10-5 C的小球套在直杆上,球与杆间的动摩擦因数为m=0.5。直杆所在处空间有水平向右的匀强电场,场强为E=106 N/C,求:
(1)小球静止起从杆的最高点A滑到最低点B时的速度大小v1;
(2)若杆与竖直方向的夹角换成不同的值,小球滑到B时的速度也会不同,为使小球滑到杆的B端时的速度最大,某同学认为应使杆沿竖直方向放置,因为这样重力做的功最多。你认为是否正确,若认为是正确的,请求出此最大速度v2,若认为不正确,请说明理由并求出此时杆与竖直方向的夹角及此最大速度v2。

(2)某同学的说法不正确(1分),因为此时虽然重力做功多了但是电场力不做功了,而且克服摩擦力做功也多了,所以末动能不是最大(1分)。为使小球到达B点时的速度最大,只要重力与电场力做的功最多而克服摩擦力做的功最小,则杆应沿重力与电场力的合力方向,即与竖直方向夹角为q’=37°,
由动能定理得:(Fesinq’+mgcosq’)L=mv22,解得v2=7.07m/s
解析:略

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
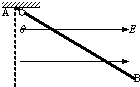 如图所示,一固定直杆AB长为L=2m,与竖直方向的夹角为θ=53°,一质量为m=4kg、电荷量为q=+3×10-5C的小球套在直杆上,球与杆间的动摩擦因数为μ=0.5.直杆所在处空间有水平向右的匀强电场,场强为E=106N/C,求:
如图所示,一固定直杆AB长为L=2m,与竖直方向的夹角为θ=53°,一质量为m=4kg、电荷量为q=+3×10-5C的小球套在直杆上,球与杆间的动摩擦因数为μ=0.5.直杆所在处空间有水平向右的匀强电场,场强为E=106N/C,求: