Question

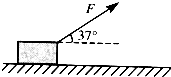如图，一质量为4.6kg的滑块，在拉力F作用下由静止开始做匀加速直线运动，其中F的方向与水平方向夹37°角，F的大小为15N．若滑块与水平面间的动摩擦因数为0.2，（g=10m/s²、sin37°=0.6、cos37°=0.8）求：
（1）滑块在力F作用下，运动的加速度大小；
（2）力F作用8s后，滑块的瞬时速度大小；
（3）如果力F作用8s后撤去，滑块在撤去F后继续滑行的距离．

Answer 1

分析：（1）物体受重力、支持力、拉力和摩擦力作用，根据牛顿第二定律求出物体的加速度大小．
（2）由速度公式求瞬时速度．
（3）先求解8s速度，然后求解撤去推力时的加速度，最后根据速度位移关系公式求解．

解答：解：（1）物体受力如图所示

由牛顿第二定律：
F_N+Fsin37°=mg
Fcos37°-μF_N=ma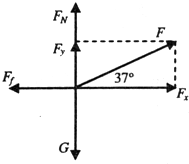                                                   
得：a=1m/s²
（2）由匀变速直线运动规律可得
V_t=V₀+at=8m/s                                               
（3）撤去外力后物体受力如图所示


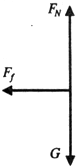
F_f=μmg=ma′
得a′=2m/s²                                     
由

V

2 t

-V

2 0

=2as，得S=16m     
答；（1）滑块在力F作用下，运动的加速度大小1m/s²；（2）力F作用8s后，滑块的瞬时速度大小8m/s；（3）如果力F作用8s后撤去，滑块在撤去F后继续滑行的距离16m．

点评：解决本题的关键知道加速度是联系力学和运动学的桥梁，通过加速度可以根据力求运动，也可以根据运动求力．