Question

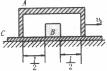
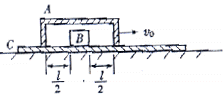
一段凹槽A倒扣在水平长木板C上，槽内有一小物块B，它到槽两侧的距离均为l/2，如图所示。木板位于光滑水平的桌面上，槽与木板间的摩擦不计，小物块与木板间的摩擦系数为μ．A、B、C三者质量相等，原来都静止．现使槽A以大小为v₀的初速向右运动，已知。当A和B发生碰撞时，两者速度互换。求：

(1)从A、B发生第一次碰撞到第二次碰撞的时间内，木板C运动的路程．

(2)在A、B刚要发生第四次碰撞时，A、B、C三者速度的大小．

 

Answer 1

答案：
解析：

解：(1)A与B刚发生第一次碰撞后，A停下不动，B以初速v0向右运动．由于摩擦，B向右作匀减速运动，而C向右作匀加速运动，两者速率逐渐接近．设B、C达到相同速度v1时B移动的路程为s1．设A、B、C质量皆为m，由动量守恒定律，得 mv0=2mv1                    ① 由功能关系，得     ② 由（1）得 代人②式，得       ③ 可见，在B、C达到相同速度v1时，B尚未与A发生第二次碰撞．B与C一起将以v1向右匀速运动一段距离（l-s1）后才与A发生第二次碰撞．设C的速度从零变到v1的过程中，C的路程为s2．由功能关系，得       ④ 因此在第一次到第二次碰撞间C的路程为   ⑤ （2）由上面讨论可知，在刚要发生第二次碰撞时，A静止，B、C的速度均为v1．刚碰撞后，B静止，A、C的速度均为v1．由于摩擦，B将加速，C将减速，直至达到相同速度v2．由动量守恒定律，得 mv1=2mv2      ⑥ 因A的速度v1大于B的速度v2，故第三次碰撞发生在A的左壁．刚碰撞后，A的速度变为v2，B的速度变为v1，C的速度仍为v2v。由于摩擦，B减速，C加速，直至达到相同速度v3.由动量守恒定律，得 mv1+mv2=2mv3      ⑦ 故刚要发生第四次碰撞时，A、B、C的速度分别为      ⑧    ⑨