题目内容
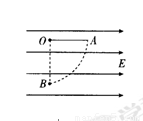
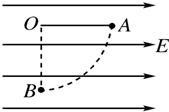 如图所示,在场强E=104N/C的水平匀强电场中,有一根长l=15cm的细线,一端固定在O点,另一端系一个质量m=3g、电荷量q=2×10-6 C的带正电小球,当细线处于水平位置时,小球从静止开始释放,g取10m/s2.求:
如图所示,在场强E=104N/C的水平匀强电场中,有一根长l=15cm的细线,一端固定在O点,另一端系一个质量m=3g、电荷量q=2×10-6 C的带正电小球,当细线处于水平位置时,小球从静止开始释放,g取10m/s2.求:(1)小球到达最低点B的过程中重力势能、电势能分别变化了多少?
(2)若取A点电势为零,小球在B点的电势能、电势分别为多大?
(3)小球到B点时速度为多大?绳子张力为多大?
分析:(1)重力势能的变化量等于重力做功的负值,电势能的变化量等于电场力做功的负值.
(2)若取A点电势为零,根据电势能的变化量,求出小球在B点的电势能.由公式φ=
求解电势.
(3)根据动能定理求出小球经过B点时的速度,由牛顿第二定律求解绳子张力.
(2)若取A点电势为零,根据电势能的变化量,求出小球在B点的电势能.由公式φ=
| EP |
| q |
(3)根据动能定理求出小球经过B点时的速度,由牛顿第二定律求解绳子张力.
解答:解:(1)小球到达最低点B的过程中重力势能的变化量为△Ep=-mgl=-4.5×10-3J,
电势能的变化量为△Ep电=Eql=3×10-3J
(2)若取A点电势为零,小球在B点的电势能Ep=△Ep电=3×10-3J
由Ep=φBq得 φB=
V=1.5×103V
(3)A→B由动能定理得:
mgl-Eql=
mvB2
代入解得vB=1m/s
在B点,对小球由牛顿第二定律得:
FT-mg=
得FT=5×10-2N
答:
(1)小球到达最低点B的过程中重力势能、电势能分别变化了-4.5×10-3J和3×10-3J.
(2)若取A点电势为零,小球在B点的电势能、电势分别为3×10-3J和1.5×103V.
(3)小球到B点时速度为1m/s,绳子张力为5×10-2N.
电势能的变化量为△Ep电=Eql=3×10-3J
(2)若取A点电势为零,小球在B点的电势能Ep=△Ep电=3×10-3J
由Ep=φBq得 φB=
| 3×10-3 |
| 2×10-6 |
(3)A→B由动能定理得:
mgl-Eql=
| 1 |
| 2 |
代入解得vB=1m/s
在B点,对小球由牛顿第二定律得:
FT-mg=
| mvB2 |
| l |
得FT=5×10-2N
答:
(1)小球到达最低点B的过程中重力势能、电势能分别变化了-4.5×10-3J和3×10-3J.
(2)若取A点电势为零,小球在B点的电势能、电势分别为3×10-3J和1.5×103V.
(3)小球到B点时速度为1m/s,绳子张力为5×10-2N.
点评:此题考查了电场力做功与电势能变化、重力做功与重力变化的关系,电势、电势能、动能定理和牛顿第二定律等规律,只要加强基础知识的学习,本题并不难.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目