题目内容
17. 在如图所示,坐标系xOy第一象限的三角形区域内(坐标如图中所标注)有垂直于纸面向外的匀强磁场,在x轴下方有沿+y方向的匀强电场,电场强度为E.将一个质量为m、电荷量为+q的粒子(重力不计)从P(0,-a)点由静止释放.由于x轴上存在一种特殊物质,使粒子每经过一次x轴速度大小变为穿过前的$\frac{\sqrt{2}}{2}$.
在如图所示,坐标系xOy第一象限的三角形区域内(坐标如图中所标注)有垂直于纸面向外的匀强磁场,在x轴下方有沿+y方向的匀强电场,电场强度为E.将一个质量为m、电荷量为+q的粒子(重力不计)从P(0,-a)点由静止释放.由于x轴上存在一种特殊物质,使粒子每经过一次x轴速度大小变为穿过前的$\frac{\sqrt{2}}{2}$.(1)欲使粒子能够再次经过x轴,求磁场的磁感应强度B0的最小值.
(2)在磁感应强度等于第(1)问中B0的情况下,求粒子在电场和磁场中运动的总时间.
分析 (1)粒子进入磁场后的轨迹圆与磁场边界相切时,磁感应强度最小为B0.由几何知识求出半径,然后由牛顿第二定律确定磁场强度;
(2)电场中运动时间由牛顿第二定律和速度公式求.画出粒子的运动轨迹,由t=$\frac{θ}{2π}$T求出磁场中运动时间.两者之和即为所求时间.
解答  解:(1)设粒子到O点时的速度为v0,由动能定理得:
解:(1)设粒子到O点时的速度为v0,由动能定理得:
qEa=$\frac{1}{2}$mv02,
解得:v0=$\sqrt{\frac{2qEa}{m}}$
粒子经过O点后,速度为v1,则:
v1=$\frac{\sqrt{2}}{2}$v0=$\sqrt{\frac{qEa}{m}}$
如图所示,粒子进入磁场后的轨迹圆与磁场边界相切时,轨迹半径最大,磁感应强度最小为B0.设粒子轨道半径为R1,有:
R1=$\sqrt{3}$a tan30°=a
由牛顿第二定律得:qB0v1=m$\frac{{v}_{1}^{2}}{{R}_{1}}$,
解得:B0=$\frac{m{v}_{1}}{q{R}_{1}}$=$\sqrt{\frac{mE}{qa}}$;
(2)如图,粒子经O1点进入电场区域做匀减速运动,后又加速返回,再次进入磁场时的速率:v2=($\frac{\sqrt{2}}{2}$)2v1=$\frac{1}{2}$v1,
则粒子在运动的时间为:t1=$\frac{{v}_{0}}{\frac{qE}{m}}$+2$\frac{{v}_{2}}{\frac{qE}{m}}$=$\sqrt{\frac{2ma}{qE}}$+2$\sqrt{\frac{ma}{qE}}$
此时粒子做圆周运动的半径:R2=$\frac{1}{2}{R}_{1}$=$\frac{1}{2}$a
其运动轨迹如图甲所示,此后不再进入磁场.由几何关系可知:∠MO1′O1=60°,
粒子在磁场中运动的周期为:T1=T2=$\frac{2πR}{v}$=$\frac{2πm}{q{B}_{0}}$=2π$\sqrt{\frac{ma}{qE}}$
粒子在磁场中运动的时间为:t2=$\frac{{T}_{1}}{2}$+$\frac{{T}_{2}}{6}$=$\frac{1}{2}•\frac{2π{R}_{1}}{{v}_{1}}$+$\frac{1}{6}•\frac{2π{R}_{2}}{{v}_{2}}$=$\frac{4π}{3}\sqrt{\frac{ma}{qE}}$;
则粒子在电场和磁场中运动的总时间为:t=t1+t2=(2+$\sqrt{2}$+$\frac{4π}{3}$)$\sqrt{\frac{ma}{qE}}$
答:(1)欲使粒子能够再次经过x轴,磁场的磁感应强度B0最小是$\sqrt{\frac{mE}{qa}}$;
(2)在磁感应强度等于第(1)问中B0的情况下,粒子在磁场中的运动时间为(2+$\sqrt{2}$+$\frac{4π}{3}$)$\sqrt{\frac{ma}{qE}}$.
点评 本题的关键是作出临界轨迹,由几何知识求轨迹半径,根据动力学方法求电场中运动时间,由圆心角求磁场中运动时间.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | 物体温度改变时,物体分子的平均动能一定改变 | |
| B. | 在两分子间距离减小的过程中,分子间引力减小,斥力增大 | |
| C. | 在两分子间距离增大的过程中,分子势能一定增大 | |
| D. | 气体压强是气体分子间的斥力产生的 |

| A. | 第4s末两物体的速度为零 | B. | 第4s内,两物体向左运动 | ||
| C. | 第2s内,拉力F对物体A做正功 | D. | 第2s内,A对B的摩擦力向左 |
| A. | 放射性的原子核在发生α衰变时,使产生的新核处于低能级,这时它要向高能级跃迁,能量以γ光子的形式辐射出来 | |
| B. | 放射性元素衰变的快慢跟原子所处的化学状态和外部条件无关 | |
| C. | 一个处于第四能级的氢原子向基态跃迁时,最多向外辐射三种不同频率的光子 | |
| D. | 普朗克通过对光电效应现象的分析提出了光子说 | |
| E. | 用某种光照射金属发生光电效应后,当光强增强时,饱和光电流会增大 |
 为了观察门外的情况,有人在门上开了一个小圆孔,将一块圆柱形玻璃嵌入其中,圆柱体轴线与门面垂直.从圆柱底面中心看去,可以看到门外入射光线与轴线间的最大夹角称为视场角.已知该玻璃的折射率为n,圆柱长为L,底面半径为r,则视场角是( )
为了观察门外的情况,有人在门上开了一个小圆孔,将一块圆柱形玻璃嵌入其中,圆柱体轴线与门面垂直.从圆柱底面中心看去,可以看到门外入射光线与轴线间的最大夹角称为视场角.已知该玻璃的折射率为n,圆柱长为L,底面半径为r,则视场角是( )| A. | arcsin$\frac{nL}{\sqrt{{r}^{2}+{L}^{2}}}$ | B. | arcsin$\frac{nr}{\sqrt{{r}^{2}+{L}^{2}}}$ | C. | arcsin$\frac{r}{n\sqrt{{r}^{2}+{L}^{2}}}$ | D. | arcsin$\frac{L}{n\sqrt{{r}^{2}+{L}^{2}}}$ |
 如图所示,长约1m的一端封闭的玻璃管中注满清水,假设t=0时刻质量为0.lkg红蜡块从玻璃管口开始运动.且每1s上升的距离都是30cm;从t=0开始,玻璃管由静止开始向右匀加速平移,第1s内、第2s内、第3s内通过的水平位移依次是5cm、15cm、25cm,则( )
如图所示,长约1m的一端封闭的玻璃管中注满清水,假设t=0时刻质量为0.lkg红蜡块从玻璃管口开始运动.且每1s上升的距离都是30cm;从t=0开始,玻璃管由静止开始向右匀加速平移,第1s内、第2s内、第3s内通过的水平位移依次是5cm、15cm、25cm,则( )| A. | t=2s时红蜡块的速度大小为0.3m/s | |
| B. | 前3s内红蜡块的位移大小为115cm | |
| C. | 红蜡块的运动是变加速曲线运动 | |
| D. | 红蜡块在上升过程中受到的合力是0.01N |
 如图所示,两根半径为r的$\frac{1}{4}$圆弧轨道间距为L,其顶端a、b与圆心处等高,轨道光滑且电阻不计,在其上端连有一阻值为R的电阻,整个装置处于辐向磁场中,圆弧轨道所在处的磁感应强度大小均为B.将一根长度稍大于L、质量为m、电阻为R0的金属棒从轨道顶端ab处由静止释放.已知当金属棒到达如图所示的cd位置(金属棒与轨道圆心连线和水平面夹角为θ)时,金属棒的速度达到最大;当金属棒到达轨道底端ef时,对轨道的压力为1.5mg.求:
如图所示,两根半径为r的$\frac{1}{4}$圆弧轨道间距为L,其顶端a、b与圆心处等高,轨道光滑且电阻不计,在其上端连有一阻值为R的电阻,整个装置处于辐向磁场中,圆弧轨道所在处的磁感应强度大小均为B.将一根长度稍大于L、质量为m、电阻为R0的金属棒从轨道顶端ab处由静止释放.已知当金属棒到达如图所示的cd位置(金属棒与轨道圆心连线和水平面夹角为θ)时,金属棒的速度达到最大;当金属棒到达轨道底端ef时,对轨道的压力为1.5mg.求:
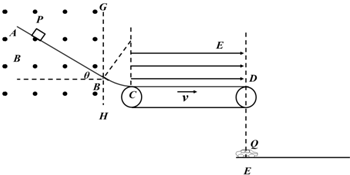 如图所示,倾角为θ=37°的粗糙斜面AB和水平传送带与半径为R=1.25m的光滑圆弧面BC分别相切于B、C两点,传送带左右两端CD的距离为L=$\frac{5}{8}$m,距水平地面的高度h=0.8m,始终以v=4m/s的速度顺时针转动;在过B点的竖直虚线GH左侧空间存在垂直纸面向外的匀强磁场,磁感应强度为B=0.4T,在传送带上方空间存在水平向右的匀强电场E=3N/C;现给质量为m=2×10-2kg、电量q=+0.1C的带电滑块P一个沿斜面向下的初速度v0其恰能在AB上匀速运动.若滑块P刚到传送带右端D点时,水平面上一质量为M=0.2kg的电动小车Q从D点正下方的E点开始以恒定功率启动,当滑块P落地时刚好击中小车且两者水平速度相等;已知小车所受阻力恒为车重的0.2倍,滑块与斜面AB和传送带间的动摩擦因素均为μ=0.5;滑块电量始终保持不变,P、Q均可视为质点,传送带转轮半径很小,取重力加速度g=10m/s2.求:
如图所示,倾角为θ=37°的粗糙斜面AB和水平传送带与半径为R=1.25m的光滑圆弧面BC分别相切于B、C两点,传送带左右两端CD的距离为L=$\frac{5}{8}$m,距水平地面的高度h=0.8m,始终以v=4m/s的速度顺时针转动;在过B点的竖直虚线GH左侧空间存在垂直纸面向外的匀强磁场,磁感应强度为B=0.4T,在传送带上方空间存在水平向右的匀强电场E=3N/C;现给质量为m=2×10-2kg、电量q=+0.1C的带电滑块P一个沿斜面向下的初速度v0其恰能在AB上匀速运动.若滑块P刚到传送带右端D点时,水平面上一质量为M=0.2kg的电动小车Q从D点正下方的E点开始以恒定功率启动,当滑块P落地时刚好击中小车且两者水平速度相等;已知小车所受阻力恒为车重的0.2倍,滑块与斜面AB和传送带间的动摩擦因素均为μ=0.5;滑块电量始终保持不变,P、Q均可视为质点,传送带转轮半径很小,取重力加速度g=10m/s2.求: