题目内容
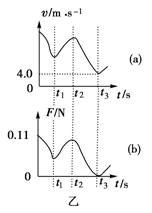
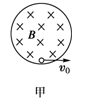
在竖直平面内有一圆形绝缘轨道，半径为R=0.4m，匀强磁场垂直于轨道平面向里，一质量为m=1×10-3 kg、带电量为q=+3×10-2 C的小球，可在内壁滑动，如图甲所示．开始时，在最低点处给小球一个初速度v0，使小球在竖直平面内逆时针做圆周运动，图乙（a）是小球在竖直平面内做圆周运动的速率v随时间变化的情况，图乙（b）是小球所受轨道的弹力F随时间变化的情况，结合图象所给数据，（取g=10m/s2）求：（1）匀强磁场的磁感应强度；
（2）小球一个初速度v0．
分析：（1）从甲图可知，小球第二次最高点时，速度大小为4m/s，而由乙图可知，此时轨道与球间的弹力为零，故由重力与洛伦兹力的合力提供向心力，根据牛顿第二定律列式，即可求得B．
（2）从图乙可知，小球第一次过最低点时，轨道与球之间弹力为F=0.11N，根据牛顿第二定律列式求解初速度v0．
（2）从图乙可知，小球第一次过最低点时，轨道与球之间弹力为F=0.11N，根据牛顿第二定律列式求解初速度v0．
解答：解：（1）从甲图可知，小球第二次最高点时，速度大小为4m/s，而由乙图可知，此时轨道与球间的弹力为零，故根据牛顿第二定律得
mg+qvB=m
代入数据得：B=0.25 T
（2）从图乙可知，小球第一次过最低点时，轨道与球之间弹力为F=0.11N，根据牛顿第二定律得：
F-mg+qv0B=m
代入数据：v0=8m/s
答：
（1）匀强磁场的磁感应强度是0.25T；
（2）小球一个初速度v0为8m/s．
mg+qvB=m
| v2 |
| R |
代入数据得：B=0.25 T
（2）从图乙可知，小球第一次过最低点时，轨道与球之间弹力为F=0.11N，根据牛顿第二定律得：
F-mg+qv0B=m
| ||
| R |
代入数据：v0=8m/s
答：
（1）匀强磁场的磁感应强度是0.25T；
（2）小球一个初速度v0为8m/s．
点评：本题解题关键是读取图象的信息，再确定小球向心力的来源，根据牛顿第二定律处理这类问题．
练习册系列答案
阅读快车系列答案
相关题目
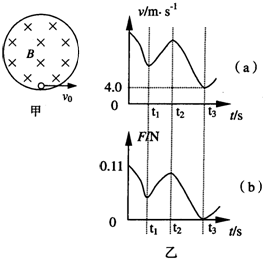
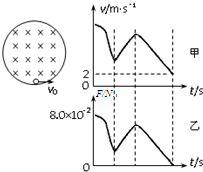在竖直平面内有一圆形绝缘轨道，半径R=1m，处于垂直于轨道平面向里的匀强磁场中，一质量为m=1×10-3kg，带电量为q=-3×10-2C的小球，可在内壁滑动．现在最低点处给小球一个水平初速度v0，使小球在竖直平面内逆时针做圆周运动，图甲是小球在竖直平面内做圆周运动的速率v随时间变化的情况，图乙是小球所受轨道的弹力F随时间变化的情况，已知小球能有两次到达圆形轨道的最高点．结合图象所给数据，g取10m/s2．求：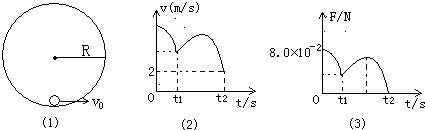
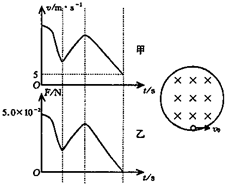在竖直平面内有一圆形绝缘轨道，半径R=1m，匀强磁场垂直于轨道平面向内，一质量m=1×10-3kg、带电量为q=+3×10-2C的小球，可在内壁滑动，开始时，在最低点处给小球一个初速度v0，使小球在竖直面内逆时针做圆周运动，图甲是小球在竖直面内做圆周的速率v随时间变化的情况，图乙是小球所受轨道的弹力F随时间变化的情况，结合图所给数据，求：
