题目内容
(14分)电子扩束装置由电子加速器、偏转电场和偏转磁场组成。偏转电场的极板由相距为d的两块水平平行放置的导体板组成,如图甲所示。大量电子由静止开始,经加速电场加速后,连续不断地沿平行板的方向从两板正中间OO'射入偏转电场。当两板不带电时,这些电子通过两板之间的时间为2t0;当在两板间加最大值为U0、周期为2t0的电压(如图乙所示)时,所有电子均能从两板间通过,然后进入竖直宽度足够大的匀强磁场中,最后打在竖直放置的荧光屏上。已知磁场的磁感应强度为B,电子的质量为m、电荷量为e,其重力不计。

(1)求电子离开偏转电场时的位置到OO'的最小距离和最大距离;
(2)要使所有电子都能垂直打在荧光屏上,
(i)求匀强磁场的水平宽度L;
(ii)求垂直打在荧光屏上的电子束的宽度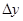 。
。

(1)求电子离开偏转电场时的位置到OO'的最小距离和最大距离;
(2)要使所有电子都能垂直打在荧光屏上,
(i)求匀强磁场的水平宽度L;
(ii)求垂直打在荧光屏上的电子束的宽度
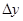 。
。(1) (2)U0t0/dB (3)
(2)U0t0/dB (3)
 (2)U0t0/dB (3)
(2)U0t0/dB (3)
试题分析:(1)由题意可知,从0、2t0、4t0、……等时刻进入偏转电场的电子离开偏转电场时的位置到OO'的距离最大,在这种情况下,电子的最大距离为:

从t0、3t0、……等时刻进入偏转电场的电子离开偏转电场时的位置到OO'的距离最小,在这种情况下,电子的最小距离为:

(2)(i)设电子从偏转电场中射出时的偏向角为q,由于电子要垂直打在荧光屏上,所以电子在磁场中运动半径应为:

设电子离开偏转电场的速度为v,垂直偏转极板的速度为vy,则电子离开偏转电场时的偏向角为:
sinθ=vy/vt,式中vy=U0et0/dm
又:R=mvt/Be
解得L=U0t0/dB
(i i)由于各个时刻从偏转电场中射出的电子的速度大小相等,方向相同,因此电子进入磁场后做圆周运动的半径也相同,都能垂直打在荧光屏上。
由第(1)问知电子离开偏转电场的位置到OO’的最大距离和最小距离的差值为:

所以垂直打在荧光屏上的电子束的宽度为:


练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )
垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )



 自O点沿水平方向射入,并恰好从P点射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。已知PA距离为d,
自O点沿水平方向射入,并恰好从P点射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。已知PA距离为d, ,
, 距离
距离 。不计带电粒子重力。
。不计带电粒子重力。
 ,电子过C、D两点时竖直方向的分速度为vCy和vDy;电子在OC段和OD动能变化量分别为△EK1和△EK2,则( )
,电子过C、D两点时竖直方向的分速度为vCy和vDy;电子在OC段和OD动能变化量分别为△EK1和△EK2,则( )




