题目内容
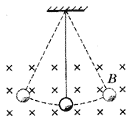
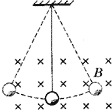
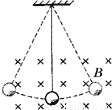
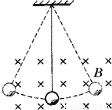
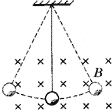如图所示，用绝缘细丝线悬吊着的带正电小球在匀强磁场中做简谐运动，则（ ）分析：小球在运动的过程中只有重力做功，洛伦兹力不做功，根据动能定理比较出通过平衡位置的动能．根据牛顿第二定律，沿半径方向的合力提供向心力，比较绳子拉力的大小．
解答：解：A、小球在运动的过程中，只有重力做功，根据动能定理得，每次经过平衡位置时，动能相同，但速度的方向不同，所以速度不同．故A正确，B错误．
C、当小球向右通过平衡位置时，根据牛顿第二定律有：T+F-mg=m
，所以T=m
+mg-F．当小球向左通过平衡位置时，根据牛顿第二定律有：T-mg-F=m
，则T=m
+F+mg，因为洛伦兹力相等，所以向左通过平衡位置时的拉力大于向右通过平衡位置时的拉力．故C错误．
D、加磁场与不加磁场，小球的速度大小一样，故周期不变．故D正确．
故选AD．
C、当小球向右通过平衡位置时，根据牛顿第二定律有：T+F-mg=m
| v2 |
| l |
| v2 |
| l |
| v2 |
| l |
| v2 |
| l |
D、加磁场与不加磁场，小球的速度大小一样，故周期不变．故D正确．
故选AD．
点评：本题综合运用了牛顿第二定律和动能定理，关键还要搞清小球做圆周运动向心力的来源．
练习册系列答案
相关题目
