题目内容
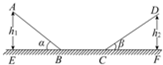 如图所示,物体从高AE=h1=2m、倾角 α=37° 的坡顶由静止开始下滑,到坡底后又经过BC=20m一段水平距离,再沿另一倾角 β=30° 的斜坡向上滑动到D处静止,DF=h2=1.75m.设物体与各段表面的动摩擦因数都相同,且不计物体在转折点B、C处的能量损失,求动摩擦因数.(取sin 37°=
如图所示,物体从高AE=h1=2m、倾角 α=37° 的坡顶由静止开始下滑,到坡底后又经过BC=20m一段水平距离,再沿另一倾角 β=30° 的斜坡向上滑动到D处静止,DF=h2=1.75m.设物体与各段表面的动摩擦因数都相同,且不计物体在转折点B、C处的能量损失,求动摩擦因数.(取sin 37°=| 3 |
| 5 |
| 4 |
| 5 |
分析:对全过程应用动能定理,即可求解动摩擦因数.
解答:解:对全过程应用动能定理得
mgh1-μmgcosα?
-mgh2-μmgcosβ?
=0-0
其中,h1=2m、α=37°、β=30°、h2=1.75m
代入解得,μ=0.01
答:动摩擦因数为0.01.
mgh1-μmgcosα?
| h1 |
| sinα |
| h2 |
| sinβ |
其中,h1=2m、α=37°、β=30°、h2=1.75m
代入解得,μ=0.01
答:动摩擦因数为0.01.
点评:本题是多过程问题,运用动能定理时,常常有两种方法,一种是分段法,另一种是全程法.本题运用全过程法比较简便.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目

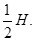 若不考虑物体经过斜面底端转折处的能量损失,则当物体再一次滑回斜面时上升的最大高度为( )
若不考虑物体经过斜面底端转折处的能量损失,则当物体再一次滑回斜面时上升的最大高度为( )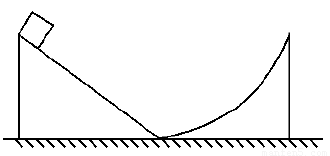
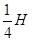
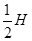 之间 D.0与
之间 D.0与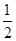 H。若不考虑物体经过斜面底端转折处的能量损失,则当物体再一次滑回斜面时上升的最大高度为
H。若不考虑物体经过斜面底端转折处的能量损失,则当物体再一次滑回斜面时上升的最大高度为
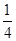 H
C.
H
C. 
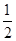 H。若不考虑物体经过斜面底端转折处的能量损失,则当物体再一次滑回斜面时上升的最大高度为
H。若不考虑物体经过斜面底端转折处的能量损失,则当物体再一次滑回斜面时上升的最大高度为
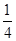 H
H