题目内容
【题目】如图所示,在水平地面上固定一倾角θ=370,表面光滑的斜面体,物体A以v1=6m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出;如果当A上滑到最高点时恰好被B物体击中.(A、B均可看做质点,sin37°=0.6,cos37°=0.8,g取10m/s2)求:
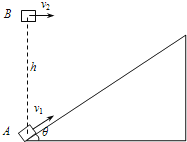
(1)物体A上滑到最高点所用的时间t;
(2)物体B抛出时的初速度v2;
(3)物体A、B间初始位置的高度差h;
【答案】(1)1 s(2)2.4 m/s(3)6.8 m
【解析】
试题分析:(1)物体A上滑的过程中,由牛顿第二定律得:mgsin θ=ma,
代入数据得:a=6 m/s2
设经过t时间B物体击中A物体,由速度公式得:0=v1-at,
代入数据得:t=1 s,
(2)A的水平位移和平抛物体B的水平位移相等:
x=![]() v1tcos 37°=2.4 m,
v1tcos 37°=2.4 m,
B做平抛运动,水平方向上是匀速直线运动,所以平抛初速度为: v2=![]() =2.4 m/s,
=2.4 m/s,
(3)物体A、B间初始位置的高度差等于A上升的高度和B下降的高度的和,所以物体A、B间的高度差为:h=![]() v1tsin 37°+
v1tsin 37°+![]() gt2=6.8 m
gt2=6.8 m

练习册系列答案
相关题目