题目内容
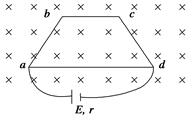
如图所示，用粗细均匀的电阻丝折成平面梯形框架，ab、cd边均与ad边成60°角，ab=bc=cd=L，长度为L的电阻丝电阻为r，框架与一电动势为E，内阻为r的电源相连接，垂直于框架平面有磁感应强度为B的匀强磁场，则框架受到的安培力的合力大小为（ ）分析：根据左手定则判断出各段受到的安培力的方向，根据闭合电路的欧姆定律计算出各段上的电流大小，再计算出各段安培力的大小，然后使用平行四边形定则合成即可．
解答：解：根据左手定则判断出各段受到的安培力的方向，如图
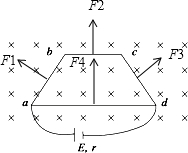
电路abcd上的电阻为3r，由几何关系得，ad段的长度为2L，所以ad上的电阻为2r，并联部分的总电阻为：R并=
=1.2r
电路中的总电流：I=
=
路端电压：U=I?R并=
?1.2r=
abcd上的电流：I1=
=
abcd上各段的安培力：F1=F2=F3=BI1L=
ad上的安培力：F4=BI2?2L=B2L
=
各段受到的力中，F1 和F3在左右方向的分量大小相等，方向相反，相互抵消，所以线框受到的合外力：F=F1cos60°+F2+F3cos60°+F4=
所以四个选项中C正确．
故选：C
电路abcd上的电阻为3r，由几何关系得，ad段的长度为2L，所以ad上的电阻为2r，并联部分的总电阻为：R并=
| 3r?2r |
| 3r+2r |
电路中的总电流：I=
| E |
| R并+r |
| E |
| 2.2r |
路端电压：U=I?R并=
| E |
| 2.2r |
| 6E |
| 11 |
abcd上的电流：I1=
| U |
| 3r |
| 2E |
| 11r |
abcd上各段的安培力：F1=F2=F3=BI1L=
| 2BEL |
| 11R |
ad上的安培力：F4=BI2?2L=B2L
| U |
| 2r |
| 6BEL |
| 11r |
各段受到的力中，F1 和F3在左右方向的分量大小相等，方向相反，相互抵消，所以线框受到的合外力：F=F1cos60°+F2+F3cos60°+F4=
| 10BEL |
| 11r |
所以四个选项中C正确．
故选：C
点评：该题中，各段时的电流的大小不相等，要使用闭合电路的欧姆定律分别计算出各段的电流的大小，然后计算安培力是解题的正确思路．题目的难度中档．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，用粗细均匀的电阻丝制成的长为2L，宽为L的矩形线框．现使线框以水平速度v向右匀速穿过一宽度为2L、磁感应强度为B的匀强磁场区域，整个过程中ab、cd两边始终与磁场边界平行．设线框的cd边刚好与磁场的左边界重合时t=0，U=2BLv，则a、b两点间电势差Uab与线框位移x的关系图象正确的是（ ）
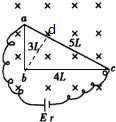如图所示，用粗细均匀的电阻丝折成平面三角形框架置于光滑水平面上，三边的长度分别为3L、4L和5L，长度为L的电阻丝的电阻为r，框架与一电动势为E、内阻不计的电源相连接，整个系统处于方向垂直于框架平面、磁感应强度为B的匀强磁场，则框架受到的安培力的合力为（ ）| A、0 | ||
B、
| ||
C、
| ||
D、
|
