题目内容
16.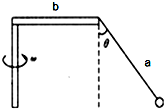 如图所示,是一游乐场中的惊险刺激的高空“飞天轮”项目的模拟示意图.已知绳长为a,水平杆长为b,小球质量为m,整个装置可绕竖直轴转动,最后保持绳子与竖直方向成θ角,重力加速度为g,试求:
如图所示,是一游乐场中的惊险刺激的高空“飞天轮”项目的模拟示意图.已知绳长为a,水平杆长为b,小球质量为m,整个装置可绕竖直轴转动,最后保持绳子与竖直方向成θ角,重力加速度为g,试求:(1)此时绳子对小球的拉力为多大?
(2)此时装置旋转的角速度为多少?
(3)该小球转动一圈的时间要多长?
分析 (1)球在竖直方向力平衡,求解绳的拉力大小;
(2)球在水平面内做匀速圆周运动,由重力mg和绳的拉力F的合力提供向心力,由牛顿第二定律求解角速度;
(3)根据T=$\frac{2π}{ω}$求解周期.
解答  解:(1)球在竖直方向力平衡,则有:
解:(1)球在竖直方向力平衡,则有:
Tcosθ=mg
解得:
$T=\frac{mg}{cosθ}$
(2)圆周运动半径r=b+asinθ
由向心力公式得:mgtanθ=mω2r
解得:$ω=\sqrt{\frac{gtanθ}{b+asinθ}}$
(3)该小球转动一圈的时间T=$\frac{2π}{ω}$=2π$\sqrt{\frac{b+asinθ}{gtanθ}}$
答:(1)此时绳子对小球的拉力为$\frac{mg}{cosθ}$;
(2)此时装置旋转的角速度为$\sqrt{\frac{gtanθ}{b+asinθ}}$;
(3)该小球转动一圈的时间为2π$\sqrt{\frac{b+asinθ}{gtanθ}}$.
点评 本题是圆锥摆问题,关键分析小球的受力情况和运动情况,容易出错的地方是圆周运动的半径r=Lsinθ,难度不大,属于基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
11.小王练习接排球.排球网高h1=2.0m,接球点距地面高h2=0.2m,距球网水平距离S=4.8m.忽略空气阻力.接球后,球刚好水平过网,则球离开小王手时的速度大小为( )
| A. | 6m/s | B. | 8m/s | C. | 10m/s | D. | 12m/s |
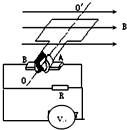
5.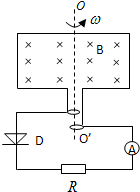 如图所示,N匝矩形导线框,以角速度ω在磁感应强度为B的匀强磁场中,绕轴OO′转动,线框面积为S,线框的电阻、电感均不计,外电路接有电阻R,理想电流表和二极管D.二极管D具有单向导电性,即正向电阻为零,反向电阻为无穷大.则下列说法正确的是( )
如图所示,N匝矩形导线框,以角速度ω在磁感应强度为B的匀强磁场中,绕轴OO′转动,线框面积为S,线框的电阻、电感均不计,外电路接有电阻R,理想电流表和二极管D.二极管D具有单向导电性,即正向电阻为零,反向电阻为无穷大.则下列说法正确的是( )
 如图所示,N匝矩形导线框,以角速度ω在磁感应强度为B的匀强磁场中,绕轴OO′转动,线框面积为S,线框的电阻、电感均不计,外电路接有电阻R,理想电流表和二极管D.二极管D具有单向导电性,即正向电阻为零,反向电阻为无穷大.则下列说法正确的是( )
如图所示,N匝矩形导线框,以角速度ω在磁感应强度为B的匀强磁场中,绕轴OO′转动,线框面积为S,线框的电阻、电感均不计,外电路接有电阻R,理想电流表和二极管D.二极管D具有单向导电性,即正向电阻为零,反向电阻为无穷大.则下列说法正确的是( )| A. | 交流电流表的示数I=$\frac{ω}{2R}$NBS | |
| B. | R两端的电压有效值为U=$\frac{ω}{\sqrt{2}}$NBS | |
| C. | 一个周期内通过R的电荷量为q=$\frac{2BS}{R}$ | |
| D. | 线框位于图示位置时,电流表的示数为0 |
6.以下叙述不正确的是( )
| A. | 伽利略在研究自由落体运动时运用了实验和逻辑推理相结合的方法 | |
| B. | 奥斯特通过理想实验,推理出电流周围存在磁场 | |
| C. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常小时,$\frac{△x}{△t}$就可以表示物体在该时刻的瞬时速度,该定义应用了极限思想方法 | |
| D. | 交流感应电动机是利用电磁驱动的原理工作的 |
 如图,匀强磁场的磁感应强度B=0.5T,边长为L=10cm的正方形线圈abcd共100匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的轴匀速转动.ω=2πrad/s,外电路电阻R=4Ω.
如图,匀强磁场的磁感应强度B=0.5T,边长为L=10cm的正方形线圈abcd共100匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的轴匀速转动.ω=2πrad/s,外电路电阻R=4Ω.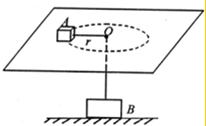 如图所示,细绳一端系着质量m=0.1kg的小物块A,置于光滑水平台面上;另一端通过光滑小孔O与质量M=0.5kg的物体B相连,B静止于水平地面上(g=10m/s2)
如图所示,细绳一端系着质量m=0.1kg的小物块A,置于光滑水平台面上;另一端通过光滑小孔O与质量M=0.5kg的物体B相连,B静止于水平地面上(g=10m/s2)