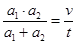题目内容
分别让一物体按照以下两种情境通过直线上的A、B两点,一种是物体以速度v匀速运动,所用时间为t;另一种是物体从A点由静止出发,先匀加速直线运动(加速度为a1)到某一最大速度vm,立即做匀减速直线运动(加速度大小为a2)至B点速度恰减为0,所用时间仍为t.下列说法正确的是( )
| A、vm只能为2v,与a1、a2的大小无关 | ||||
| B、vm可为许多值,与a1、a2的大小有关 | ||||
| C、a1、a2必须是一定的 | ||||
D、a1、a2必须满足
|
分析:两次运动总位移相等、总时间相等,则平均速度相等,结合匀变速直线运动的推论求解匀加速直线运动的最大速度.
解答:解:两次运动过程平均速度相等,知平均速度的大小为v.
根据匀变速直线运动的推论知,
t1+
t2=
t=x,则vm=
=2v,与加速度大小无关.故A正确,B、C、D错误.
故选:A.
根据匀变速直线运动的推论知,
| vm |
| 2 |
| vm |
| 2 |
| vm |
| 2 |
| 2x |
| t |
故选:A.
点评:解决本题的关键掌握匀变速直线运动平均速度的推论
=
,并能灵活运用.
. |
| v |
| v0+v |
| 2 |

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 (1)探究力对原来静止的物体做功与物体获得的速度的关系,实验装置如图所示,实验主要过程如下:
(1)探究力对原来静止的物体做功与物体获得的速度的关系,实验装置如图所示,实验主要过程如下:
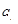 )到某一最大速度
)到某一最大速度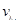 ,立即做匀减速直线运动(加速度大小为a2)至B点速度恰减为0,所用时间仍为t。下列说法正确的是
,立即做匀减速直线运动(加速度大小为a2)至B点速度恰减为0,所用时间仍为t。下列说法正确的是