题目内容
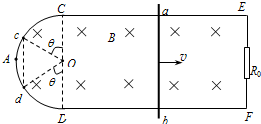 如图所示,ECADF为水平光滑金属轨道,其中EC、FD段相互平行,足够长且电阻不计;CAD段是一半圆弧,O是圆心,其半径r=0.5m、电阻R1=24Ω;E、F端用导线接有阻值R0=8Ω的电阻.整个轨道处在磁感强度B=2T的竖直向下的匀强磁场中.金属棒ab质量m=0.5kg,其电阻为零,横跨在轨道上且保持与轨道接触良好;棒在水平外力作用下,从轨道的顶点A开始沿轨道匀速向右滑动,速度v=6m/s.
如图所示,ECADF为水平光滑金属轨道,其中EC、FD段相互平行,足够长且电阻不计;CAD段是一半圆弧,O是圆心,其半径r=0.5m、电阻R1=24Ω;E、F端用导线接有阻值R0=8Ω的电阻.整个轨道处在磁感强度B=2T的竖直向下的匀强磁场中.金属棒ab质量m=0.5kg,其电阻为零,横跨在轨道上且保持与轨道接触良好;棒在水平外力作用下,从轨道的顶点A开始沿轨道匀速向右滑动,速度v=6m/s.(1)当ab棒通过图中c、d两点时(c、d两点位置如图中所示,θ=60°),计算R0此时刻的电功率;
(2)当ab棒在CE段运动时,求水平拉力做功的功率.
分析:(1)当ab棒通过图中c、d两点时,棒产生的感应电动势E1=BLcdv,由欧姆定律求得R0分得的电压,即可求出其功率.
(2)当ab棒在CE段运动时,棒产生的感应电动势E2=2Brv,求出外电路总电阻,由欧姆定律求得ab棒内的电流I,ab棒所受安培力为FB=2BrI,由于匀速运动,水平外力跟安培力平衡,得到外力的大小,即可求得外力功率P=Fv.
(2)当ab棒在CE段运动时,棒产生的感应电动势E2=2Brv,求出外电路总电阻,由欧姆定律求得ab棒内的电流I,ab棒所受安培力为FB=2BrI,由于匀速运动,水平外力跟安培力平衡,得到外力的大小,即可求得外力功率P=Fv.
解答:解:(1)当ab棒通过图中c、d两点时,cd间的长度为Lcd=r=0.5m,棒产生的感应电动势E1=BLcdv=6V
由于ab没有电阻,RCc=RdD=8Ω,R0=8Ω,则R0分得的电压U0=
E1=
×6=2V
R0的电功率P0=
=
=0.5W
(2)当ab棒在CE段运动时,棒产生的感应电动势E2=2Brv=2×2×0.5×6=12V
外电路的总电阻R=
=
=6Ω
ab棒内电流为I=
=
=2A
ab棒所受安培力为FB=2BrI=2×2×0.5×2=4N
ab棒匀速运动,水平外力跟安培力平衡,则 F=FB=4N
所以F的功率P=Fv=4×6W=24W
答:(1)当ab棒通过图中c、d两点时R0此时刻的电功率是0.5W;
(2)当ab棒在CE段运动时,水平拉力做功的功率是24W.
由于ab没有电阻,RCc=RdD=8Ω,R0=8Ω,则R0分得的电压U0=
| 8 |
| 24 |
| 1 |
| 3 |
R0的电功率P0=
| ||
| R0 |
| 22 |
| 8 |
(2)当ab棒在CE段运动时,棒产生的感应电动势E2=2Brv=2×2×0.5×6=12V
外电路的总电阻R=
| R1R0 |
| R1+R0 |
| 24×8 |
| 24+8 |
ab棒内电流为I=
| E2 |
| R |
| 12 |
| 6 |
ab棒所受安培力为FB=2BrI=2×2×0.5×2=4N
ab棒匀速运动,水平外力跟安培力平衡,则 F=FB=4N
所以F的功率P=Fv=4×6W=24W
答:(1)当ab棒通过图中c、d两点时R0此时刻的电功率是0.5W;
(2)当ab棒在CE段运动时,水平拉力做功的功率是24W.
点评:本题是电磁感应与电路知识的综合应用,要结合电路的结构,运用法拉第定律、欧姆定律等等基本规律求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
