题目内容
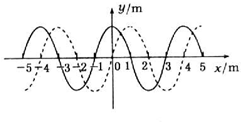
如图所示,实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.(1)假定波向左传播,求它传播的可能距离.
(2)若这列波向右传播,求它的最大周期.
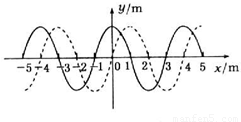
【答案】分析:(1)假定波向左传播时,波传播的最短距离为 波长,根据周期性列出波传播的可能距离.
波长,根据周期性列出波传播的可能距离.
(2)若这列波向右传播,根据周期性得出时间与周期的关系通项式,再求解最大周期.
解答:解:(1)向左传播时的距离为
S=(n+ )λ=4(n+
)λ=4(n+ )m=(4n+3)m,(n=0,1,2…).
)m=(4n+3)m,(n=0,1,2…).
(2)若这列波向右传播,则有
t=(n+ )T,得
)T,得
周期T= ,(n=0,1,2…).在所有可能的周期中,当n=0时的最大,故Tmax=0.8s.
,(n=0,1,2…).在所有可能的周期中,当n=0时的最大,故Tmax=0.8s.
答:
(1)假定波向左传播,它传播的可能距离为(4n+3)m,(n=0,1,2…).
(2)若这列波向右传播,它的最大周期为0.8s.
点评:本题知道两个时刻的波形,若限制条件得到波传播距离的通项,再求解特殊值.
 波长,根据周期性列出波传播的可能距离.
波长,根据周期性列出波传播的可能距离.(2)若这列波向右传播,根据周期性得出时间与周期的关系通项式,再求解最大周期.
解答:解:(1)向左传播时的距离为
S=(n+
 )λ=4(n+
)λ=4(n+ )m=(4n+3)m,(n=0,1,2…).
)m=(4n+3)m,(n=0,1,2…).(2)若这列波向右传播,则有
t=(n+
 )T,得
)T,得周期T=
 ,(n=0,1,2…).在所有可能的周期中,当n=0时的最大,故Tmax=0.8s.
,(n=0,1,2…).在所有可能的周期中,当n=0时的最大,故Tmax=0.8s.答:
(1)假定波向左传播,它传播的可能距离为(4n+3)m,(n=0,1,2…).
(2)若这列波向右传播,它的最大周期为0.8s.
点评:本题知道两个时刻的波形,若限制条件得到波传播距离的通项,再求解特殊值.

练习册系列答案
相关题目
 如图所示,实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.
如图所示,实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.