题目内容
如图所示，从倾角为θ的足够长的斜面A点先将小球以速度V1水平向右抛出，球落到斜面上前一瞬间的速度方向与斜面夹角为α1。然后在B点以速度V2（V1>V2）水平向右抛出，球落到斜面上前一瞬间的速度方向与斜面夹角为α2，则：
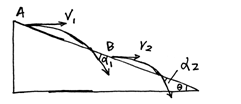
| A．α1>α2 | B．α1<α2 |
| C．α1=α2 | D．无法确定 |
C
分析：设小球落在斜面上时平抛初速度为v0，落在斜面底端时初速度为v1，落在水平面上C点时初速度为v2．小球落在斜面上时，斜面倾角的正切等于竖直位移与水平位移之比，列式求出平抛运动的时间，再求出落在斜面时速度方向与水平方向的夹角的正切，来比较夹角的大小．
解答：解：设小球落在斜面上时平抛初速度为v0，落在斜面上时速度与水平方向的夹角为θ′，斜面倾角为θ．由tanθ=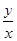
=
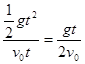，得到t=
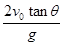，则tanθ′=
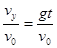=2tanθ，与初速度大小无关，即落到斜面上时速度方向与水平方向的夹角均相等，所以α1=α2．
故选C
点评：本题关键是斜面的倾角的应用，它表示位移方向与水平方向的夹角，分解位移，不是分解速度，不能得到这样的式子：tanθ=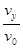
．
解答：解：设小球落在斜面上时平抛初速度为v0，落在斜面上时速度与水平方向的夹角为θ′，斜面倾角为θ．由tanθ=
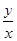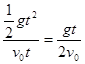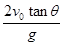=，得到t=，则tanθ′=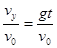=2tanθ，与初速度大小无关，即落到斜面上时速度方向与水平方向的夹角均相等，所以α1=α2．故选C
点评：本题关键是斜面的倾角的应用，它表示位移方向与水平方向的夹角，分解位移，不是分解速度，不能得到这样的式子：tanθ=
．
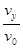练习册系列答案
相关题目
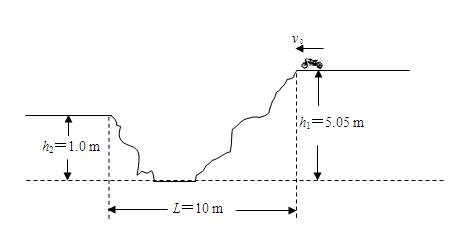
沿水平方向飞向另一侧，壕沟的宽度及两侧的高度如图所示（不计空气阻力，取g =" 10" m/s2，可能用到的三角函数值为sin30°= 0.50、sin37°= 0.60、sin45°= 0.71、sin60°= 0.87、sin90° = 1.0）。
