题目内容
如图所示,置于竖直平面内的AB光滑杆,它是以初速为v0,水平射程为s的平抛运动轨迹制成的,A端为抛出点,B端为落地点.现将一质量为m的小球套于其上,由静止开始从轨道A端滑下,重力加速度为g.则当其到达轨道B端时
| A.小球在水平方向的速度大小为v0 |
B.小球运动的时间为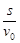 |
C.小球的速率为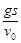 |
D.小球重力的功率为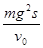 |
C
解析试题分析:据题意,小球受到重力G和支持力N,所以小球由静止从光滑杆上滑下的运动不是平抛运动,则小球在水平方向的分速度也是变化的,所以小球在水平方向的分速度不等于v0,A选项错误;小球的运动时间也不等于t="s/" v0,所以B选项错误;小球机械能守恒,有mgh=mv2/2,由于光滑杆是按照平抛运动的轨迹制定的,所以轨迹遵循平抛运动规律,则有tanθ="2tana," a是位移偏向角,θ速度偏向角,tanθ=vy/vx, vy= 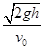 ,vx= v0,而tanα=y/x,y=gt2/2,x=s,联立求得h=
,vx= v0,而tanα=y/x,y=gt2/2,x=s,联立求得h= 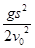 ,合速度v=
,合速度v= 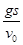 ,C选项正确;小球重力的功率为P="mgvsinθ="
,C选项正确;小球重力的功率为P="mgvsinθ="  ,所以D选项错误。
,所以D选项错误。
考点:本题考查机械能守恒定律,平抛运动的应用。

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案物体以40m/s的初速度竖直上抛,不计空气阻力,g取10m/s2。5秒内,关于物体的运动,下列说法中正确的是( )
| A.路程为90m |
| B.位移大小为75m,方向向上 |
| C.速度改变量为30m/s,方向向下 |
| D.平均速度为25m/s,方向向上 |
做平抛运动的物体,每秒的动量增量总是
| A.大小相等方向相同 | B.大小不等方向不同 |
| C.大小相等方向不同 | D.大小不等方向相同 |
如图所示,斜面上O、P、Q、R、S五个点,距离关系为 ,从O点以υ0的初速度水平抛出一个小球,不计空气阻力,小球落在斜面上的P点.若小球从O点以2υ0的初速度水平抛出,则小球将落在斜面上的 ( )
,从O点以υ0的初速度水平抛出一个小球,不计空气阻力,小球落在斜面上的P点.若小球从O点以2υ0的初速度水平抛出,则小球将落在斜面上的 ( )
| A.Q点 | B.S点 | C.Q、R两点之间 | D.R、S两点之间 |
在同一水平直线上的两位置分别沿同方向抛出两小球 和
和 ,其运动轨迹如图所示,不计空气阻力.要使两球在空中相遇,则必须
,其运动轨迹如图所示,不计空气阻力.要使两球在空中相遇,则必须 
A.甲先抛出 球 球 | B.先抛出 球 球 |
| C.同时抛出两球 | D.使两球质量相等 |
平抛运动可以分解为水平和竖直两个方向的直线运动,在同一坐标系中作出这两个分运动的v-t图像,如图所示,若平抛运动的时间大于2t1, g=10m/s2, 则下列说法中正确的是: 
| A.图线1表示竖直分运动的v-t图线 |
| B.图线2表示水平分运动的v-t图线 |
| C.t1时间内物体速度的变化量大小为20t1(m/s),方向与水平方向成450 |
| D.t1时刻的速度方向与初速度方向夹角为45° |
 ,射程为
,射程为 的平抛运动轨迹制成一光滑轨道。一物体由静止开始从轨道顶端滑下,当其到达轨道底部时,物体水平方向速度大小为
的平抛运动轨迹制成一光滑轨道。一物体由静止开始从轨道顶端滑下,当其到达轨道底部时,物体水平方向速度大小为



 、
、 、
、 的关系和三个物体做平抛运动的时间
的关系和三个物体做平抛运动的时间 、
、 、
、 的关系分别是
的关系分别是 




