题目内容
4.设地球的质量为M,平均半径为R,自转角速度为ω,引力常量为G,则同步卫星的离地高度为多少.分析 同步卫星的周期与地球自转周期相同,卫星绕地球做圆周运动万有引力提供向心力,由牛顿第二定律可以求出卫星半径,然后求出高度.
解答 解:同步卫星的角速度与地球自转的角速度相等,卫星绕地球做圆周运动,万有引力提供向心力,由牛顿第二定律得:
G$\frac{Mm}{{r}^{2}}$=mω2r,
解得:r=$\root{3}{\frac{GM}{{ω}^{2}}}$,
同步卫星距地面的高度:h=r-R=$\root{3}{\frac{GM}{{ω}^{2}}}$-R;
答:同步卫星离地的高度为$\root{3}{\frac{GM}{{ω}^{2}}}$-R.
点评 本题考查了万有引力定律的应用,知道万有引力提供向心力、应用万有引力公式与牛顿第二定律可以解题,解题时注意:同步卫星的角速度与地球自转的角速度相等.

练习册系列答案
相关题目
14. 均匀的长杆斜靠在光滑的竖直墙上,当杆与墙成θ=37°时杆平衡状态,则地面与杆间的动摩擦因数应满足(tanθ=$\frac{3}{4}$)( )
均匀的长杆斜靠在光滑的竖直墙上,当杆与墙成θ=37°时杆平衡状态,则地面与杆间的动摩擦因数应满足(tanθ=$\frac{3}{4}$)( )
 均匀的长杆斜靠在光滑的竖直墙上,当杆与墙成θ=37°时杆平衡状态,则地面与杆间的动摩擦因数应满足(tanθ=$\frac{3}{4}$)( )
均匀的长杆斜靠在光滑的竖直墙上,当杆与墙成θ=37°时杆平衡状态,则地面与杆间的动摩擦因数应满足(tanθ=$\frac{3}{4}$)( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{4}{5}$ |
12.下列情形中,两物体分子数相同的条件是( )
| A. | 两物体质量相同 | B. | 两物体体积相同 | ||
| C. | 两物体摩尔质量相同 | D. | 两物体摩尔数相同 |
9.某同学非常勤于物理思考.一次,该同学对自行车打气,在打气筒缓慢下压的过程中,得出车胎内气体的几种说法,你认为正确的说法是( )
| A. | 气体内能减小,放出热量 | B. | 气体对外做功,温度升高 | ||
| C. | 气体体积减小,吸收热量 | D. | 气体压强增大,内能几乎不变 |
16. 如图所示,a、b是两个带有同种电荷的小球,用绝缘细线系于同一点.两球静止时它们在同一水平面上,与竖直方向的夹角依次为α=30°和β=60°.若同时剪断细线,不计空气阻力,则下列说法中正确的是( )
如图所示,a、b是两个带有同种电荷的小球,用绝缘细线系于同一点.两球静止时它们在同一水平面上,与竖直方向的夹角依次为α=30°和β=60°.若同时剪断细线,不计空气阻力,则下列说法中正确的是( )
 如图所示,a、b是两个带有同种电荷的小球,用绝缘细线系于同一点.两球静止时它们在同一水平面上,与竖直方向的夹角依次为α=30°和β=60°.若同时剪断细线,不计空气阻力,则下列说法中正确的是( )
如图所示,a、b是两个带有同种电荷的小球,用绝缘细线系于同一点.两球静止时它们在同一水平面上,与竖直方向的夹角依次为α=30°和β=60°.若同时剪断细线,不计空气阻力,则下列说法中正确的是( )| A. | a、b两小球落地瞬间a小球重力的瞬时功率小于b球重力的瞬时功率 | |
| B. | 下落过程中a小球水平飞行的距离比b球大 | |
| C. | 下落过程中a、b两小球受到的冲量大小相同 | |
| D. | a、b两小球将同时落在地面上 |
13.下列关于质点的一些说法,其中正确的是( )
| A. | 研究和观察日食时,可以把太阳看成质点 | |
| B. | 原子核很小,一定可把它看成质点 | |
| C. | 研究地球自转时,不能把地球看成质点 | |
| D. | 做花样溜冰的运动员一定可以看作质点 |
14.如图1所示,是某研究性学习小组做探究“橡皮筋做的功和物体速度变化的关系”的实验,图中是小车在一条橡皮筋作用下弹出,沿木板滑行的情形,这时,橡皮筋对小车做的功记为W.当我们用2条、3条…完全相同的橡皮筋并在一起进行第2次、第3次…实验时,每次橡皮筋都拉伸到同一位置释放.小车每次实验中获得的速度由打点计时器所打的纸带测出.

(1)除了图中的已给出的实验器材外,还需要的器材有交流电源、刻度尺;
(2)实验时为了使小车只在橡皮筋作用下运动,应采取的措施是把木板的末端垫起适当高度以平衡摩擦力;
(3)每次实验得到的纸带上的点并不都是均匀的,为了测量小车获得的速度,应选用纸带的点距均匀部分进行测量;
(4)下面是本实验的数据记录表,请将第2次、第3次…实验中橡皮筋做的功填写在对应的位置;
(5)从理论上讲,橡皮筋做的功Wn和物体速度vn变化的关系应是Wn∝v2.请你运用数据表中测定的数据在图2所示的坐标系中作出相应的图象验证理论的正确性.

(1)除了图中的已给出的实验器材外,还需要的器材有交流电源、刻度尺;
(2)实验时为了使小车只在橡皮筋作用下运动,应采取的措施是把木板的末端垫起适当高度以平衡摩擦力;
(3)每次实验得到的纸带上的点并不都是均匀的,为了测量小车获得的速度,应选用纸带的点距均匀部分进行测量;
(4)下面是本实验的数据记录表,请将第2次、第3次…实验中橡皮筋做的功填写在对应的位置;
| 橡皮筋做的功 | 10个间隔的距离S(m) | 10个间隔的时间T(s) | 小车获得的速度vn(m/s) | 小车速度的平方vn2(m/s)2 | |
| 1 | W | 0.200 | 0.2 | ||
| 2 | 0.280 | 0.2 | |||
| 3 | 0.300 | 0.2 | |||
| 4 | 0.400 | 0.2 | |||
| 5 | 0.450 | 0.2 |
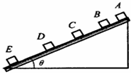 一个质量为m的物块由静止开始沿斜面下滑,拍摄此下滑过程得到的同步闪光(即第一次闪光时物块恰好开始下滑)照片如图所示.已知闪光频率为每秒10次,根据照片测得物块相邻两位置之间的距离分别为AB=2.40cm,BC=7.30cm,CD=12.20cm,DE=17.10cm.由此可知,物块经过D点时的速度大小为1.47m/s;若此斜面的倾角θ为37°,则物块与斜面间的动摩擦因数为0.14.(取g=9.80m/s2,sin37°=0.600,cos37°=0.800,保留3位有效数字)
一个质量为m的物块由静止开始沿斜面下滑,拍摄此下滑过程得到的同步闪光(即第一次闪光时物块恰好开始下滑)照片如图所示.已知闪光频率为每秒10次,根据照片测得物块相邻两位置之间的距离分别为AB=2.40cm,BC=7.30cm,CD=12.20cm,DE=17.10cm.由此可知,物块经过D点时的速度大小为1.47m/s;若此斜面的倾角θ为37°,则物块与斜面间的动摩擦因数为0.14.(取g=9.80m/s2,sin37°=0.600,cos37°=0.800,保留3位有效数字)