题目内容
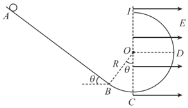
【题目】如图，在竖直平面内有一固定光滑轨道ABCDI，其中斜面AB与圆心为O的圆弧轨道相切于B点，C、D分别为圆弧轨道的最低点、最右点，OB与OC夹角
= 37°，在OC所在直线的右侧有沿OD方向的匀强电场.现将一质量为m、电荷量为q的带正电小球从与B点相距为2R的A点静止释放，沿轨道滑下.巳知场强大小E=
，重力加速度大小为g，取sin37°= 0. 6，cos37°=0.8.求：
（1）小球从A点运动到B点所用的时间；
（2）小球到达D点时的速度大小；
（3）小球在圆弧轨道上运动的过程中，轨道对小球支持力的最大值FNm.
【答案】（1）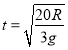
（2）
（3）
【解析】
（1）小球在AB段运动时，由牛顿第二定律：
从A到B，与运动公式：
联立解得：
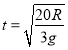
（2）从A到D由动能定理：
解得：
（3）设小球运动到M点时对轨道的压力最大；
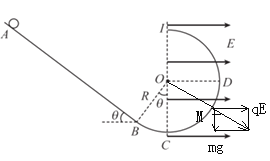
此位置应该是小球的平衡位置，设OM与竖直方向夹角为α，则
重力和电场力的合力为
从M点到D点，由动能定理：
解得：
在D点，由牛顿第二定律：
解得
练习册系列答案
阅读快车系列答案
相关题目
