Question

【题目】已知某星球的半径为R，有一距星球表面高度h=R处的卫星，绕该星球做匀速圆周运动，测得其周期T=2π ．

（1）求该星球表面的重力加速度g；
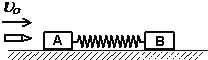
（2）若在该星球表面有一如图的装置，其中AB部分为一长为L=10m并以v=3.2m/s速度顺时针匀速转动的水平传送带，BCD部分为一半径为r=1.0m竖直放置的光滑半圆形轨道，直径BD恰好竖直，并与传送带相切于B点．现将一质量为m=1.0kg的可视为质点的小滑块无初速地放在传送带的左端A点上，已知滑块与传送带间的动摩擦因数为μ=0.5．求：①质点到B点的速度；②质点到达D点时受轨道作用力的大小（注：取 =2）．

Answer 1

【答案】
（1）解：对距星球表面h=R处的卫星（设其质量为m），

有：

对在星球表面的物体m′，有：

解得：g=1.6 m/s2

答：星球表面的重力加速度为1.6 m/s2

（2）解：设滑块从A到B一直被加速，且设到达B点时的速度为vB则：

m/s

因vB＞3.2m/s，故滑块一直被加速到3.2m/s，然后做匀速直线运动；

设滑块能到达D点，且设到达D点时的速度为vD

则在B到D的过程中，由动能定理：﹣mg2r= mvD2﹣ mvB2

解得：vD= m/s≈2m/s

而滑块能到达D点的临界速度：v0= =1.26m/s＜VD

即滑块能到达D点

在D点时由重力和轨道的压力共同提供向心力：

N+mg=

解得：

N=2.4N

由牛顿第三定律知，物体对轨道的压力为2.4N

答：①质点到B点的速度是2m/s；②在D点对轨道的压力为2.4N．

【解析】（1）由卫星在高处的周期，可以力万有引力提供向心力的周期表达式，在联合在星球表面万有引力等于重力，可以解得星球重力加速度∴（2）首先解决物体到B点的速度问题，在传送带上先按照物体已知被加速度来做，看到B的速度是否大于传送带速度，若不小于，则说明假设是正确的，可以求出物体的加速度，若大于，说明假设，不对，物体没有一直被加速，需要再讨论，求出B点的速度后，再判断物体能否到达D点，进而才能确定是否有压力，压力大小是多少．
【考点精析】解答此题的关键在于理解万有引力定律及其应用的相关知识，掌握应用万有引力定律分析天体的运动：把天体的运动看成是匀速圆周运动，其所需向心力由万有引力提供.即 F引=F向；应用时可根据实际情况选用适当的公式进行分析或计算.②天体质量M、密度ρ的估算．