题目内容
12.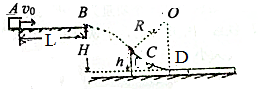 如图所示,一质量m=1kg的小物块从A点被以v0=8m/s的水平速度弹出,沿着滑动摩擦因数μ0=0.6的粗糙水平面运动做直线运动,物块经过B点后水平抛出,AB间距离L=4m,当物块运动至C点时,恰好沿切线方向进入固定光滑圆弧轨道CD,经圆弧轨道后滑上与D点等高、静止在粗糙水平面的长木板上,圆弧轨道D端切线水平,已知长木板的质量M=4kg,B、C两点距D点的高度分别为H=0.6m,h=0.15m,R=0.75m,物块与长木板之间的动摩擦因数μ1=0.5,长木板与地面间的动摩擦因数μ2=0.2,g=10m/s2,求:
如图所示,一质量m=1kg的小物块从A点被以v0=8m/s的水平速度弹出,沿着滑动摩擦因数μ0=0.6的粗糙水平面运动做直线运动,物块经过B点后水平抛出,AB间距离L=4m,当物块运动至C点时,恰好沿切线方向进入固定光滑圆弧轨道CD,经圆弧轨道后滑上与D点等高、静止在粗糙水平面的长木板上,圆弧轨道D端切线水平,已知长木板的质量M=4kg,B、C两点距D点的高度分别为H=0.6m,h=0.15m,R=0.75m,物块与长木板之间的动摩擦因数μ1=0.5,长木板与地面间的动摩擦因数μ2=0.2,g=10m/s2,求:(1)小物块运动至C点时的速度大小和方向;
(2)小物块滑动至D点时,对圆弧轨道D点的压力;
(3)长木板至少为多长,才能保证小物块不滑出长木板?
分析 (1)已知平抛的抛出高度和落地速度方向,求落地的速度大小和方向,用运动的合成与分解求解;
(2)小物块在BC间做圆周运动运动,在C点时轨道支持力和重力的合力提供圆周运动的向心力,据此求解即可;
(3)根据物块在长木板上滑动时,物块的位移-长木板的位移应该小于等于长木板的长度这一临界条件展开讨论即可
解答 解:(1)物体到达B点的速度为v,在Ab段由动能定理可得${μ}_{0}mgL=\frac{1}{2}m{v}^{2}-\frac{1}{2}{mv}_{0}^{2}$
解得v=4m/s
物块做平抛运动:H-h=$\frac{1}{2}$gt2
设到达D点时竖直分速度为vy则:vy=gt
v1=$\sqrt{{v}^{2}{+v}_{y}^{2}}$=$\frac{5}{4}$v=5m/s
方向与水平面的夹角为θ:tanθ=$\frac{{v}_{y}}{v}$=0.75,即θ=37°
(2)从B至D点,由动能定理得mgH=$\frac{1}{2}{mv}_{1}^{2}-\frac{1}{2}m{v}^{2}$ ①
设D点受到的支持力为FN,则有FN-mg=m$\frac{{v}_{1}^{2}}{R}$
由①式可得v2=2$\sqrt{7}$m/s
所以:FN=47.3 N
根据牛顿第三定律可知,物块m对圆弧轨道C点的压力大小为47.3N
(3)由题意可知小物块m对长木板的摩擦力f=μ1mg=5N
长木板与地面间的最大静摩擦力近似等于滑动摩擦力f′=μ2(M+m)g=10N
因f<f′,所以小物块在长木板上滑动时,长木板静止不动
小物块在长木板上做匀减速运动,至长木板右端时速度刚好为0
则长木板长度至少为l=$\frac{{v}_{1}^{2}}{2{μ}_{1}g}$=2.8m
答:(1)小物块运动至C点时的速度大小为5m/s,方向与水平面成37°角;
(2)小物块滑动至D点时,对圆弧轨道C点的压力FN=47.3 N;
(3)长木板至少为2.8m,才能保证小物块不滑出长木
点评 本题关键要理清物块在多个不同运动过程中的运动规律,掌握物块各个阶段的运动规律是解决本题的关键

| A. | 0 | B. | 16J | C. | 48J | D. | 64J |
| A. | 滑动摩擦力阻碍物体的相对运动,所以一定做负功 | |
| B. | 静摩擦力虽然阻碍物体间的相对运动,但不做功 | |
| C. | 静摩擦力和滑动摩擦力不一定都做负功 | |
| D. | 一对相互作用力,若作用力做正功,则反作用力一定做负功 |
| A. | 电磁波只能在真空中传播 | |
| B. | 电场随时间变化时一定产生电磁波 | |
| C. | 变化的磁场周围会产生电场 | |
| D. | 麦克斯韦第一次用实验证实了电磁波的存在 |
| A. | 磁场周围一定存在电场 | |
| B. | 电场周围一定存在磁场 | |
| C. | 点电荷的电场周围一定没有磁场 | |
| D. | 变化的磁场周围不一定存在变化的电场 |
| A. | 平抛运动是匀速运动 | |
| B. | 平抛运动是加速度不变的运动 | |
| C. | 平抛运动是加速度变化的运动 | |
| D. | 平抛运动落地时速度可能是竖直向下的 |
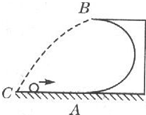 如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则小球在B点的速度是$\sqrt{gR}$,小球落地点C到A的距离是2R.
如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则小球在B点的速度是$\sqrt{gR}$,小球落地点C到A的距离是2R.