题目内容
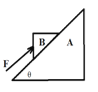
【题目】如图所示，倾角为
37°的固定斜面与足够长的水平面平滑对接，一劲度系数k=18N/m的轻质弹簧的上端固定于斜面顶端，另一端固定连接在一质量m=1kg的光滑小球A上，跟小球紧靠的物块B（质量也为m）与斜面间的动摩擦因数
=0．75，且最大静摩擦力等于滑动摩擦力，与水平面间的动摩擦因数
=0．1，图中施加在物块上的力F=18N，方向沿斜面向上，A和B均处于静止状态，且斜面对B恰无摩擦力，当撤掉F，A和B一起沿斜面下滑到木处分离，分离后A一直在斜面上运动，B继续沿斜面下滑，已知sin37°=0．6，cos37°=0．8，重力加速度
（1）A和B分离后A能否再回到出发点？请简述理由。
（2）A和B分离时B的速度为多大？
（3）求B最终停留的位置距斜面底端多远？
【答案】（1）不能（2）
（3）
【解析】
试题分析：（1）A不能回到出发点，因为小球与物块一起下滑过程，物体对小球的弹力做负功而使小球和弹簧的机械能减少
（2）未撤去力F时，对A和B整体，根据平衡条件得：
，其中弹力为：
解得弹簧的压缩量为：
分离时，AB之间无弹力作用，但速度和加速度相等，根据牛顿第二定律，
对B：
，其中
，联立解得
对A：
，其中弹力
由
，解得分离时弹簧的伸长量为：
可见
，AB整体运动到分离弹簧的弹力做功为零，根据动能定理有：
带入数据解得：
（3）分离后由动能定理得：
,代入数据解得：
练习册系列答案
相关题目
