题目内容
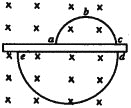
【题目】如图所示,MN是半径为R=0.8m的竖直四分之一光滑圆弧轨道,竖直固定在水平桌面上,轨道末端处于桌子边缘并与水平桌面相切于N点。把一质量为m=1kg的小球B静止放于N点,另一个完全相同的小球A由M点静止释放,经过N点时与B球发生正碰,碰后粘在一起水平飞出,落在地面上的碰点。若桌面高度为h=0.8m,取重力加速度g=10m/![]() 。不计空气阻力,小球可视为质点。求:
。不计空气阻力,小球可视为质点。求:

(1)小球A运动到N点与小球B碰前的速度![]() 的大小;
的大小;
(2)小球A与小球B碰后瞬间的共同速度![]() 的大小;
的大小;
(3)P点与N点之间的水平距离x.
【答案】(1)4m/s(2)2m/s(3)0.8m
【解析】
(1)小球在圆弧轨道内下滑过程中,由动能定理即可求出;
(2)小球到达N点,与B发生碰撞,由动量守恒定律即可求出碰撞后的速度;
(3)由平抛运动规律即水平方向上匀速和竖直方向自由落体可求水平距离。
(1)小球在圆弧轨道内下滑过程中,由动能定理得:
![]()
代入数据解得:
![]() ;
;
(2)两个小球碰撞的过程中水平方向的动量守恒,选取向右为正方向,设碰撞后的共同速度为v,则:
![]()
代入数据可得:
![]()
(3)小球从N点飞出后做平抛运动,
![]()
竖直方向上:
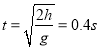
水平方向上:
![]()
解得:
![]() 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目