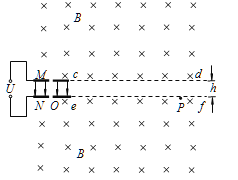题目内容
【题目】示波器中的示波管对电子的偏转是电偏转，电视机中的显像管对电子的偏转是磁偏转。小明同学对这两种偏转进行了定量的研究并做了对比，已知电子的质量为m、电荷量为e，在研究的过程中空气阻力和电子所受重力均可忽略不计。
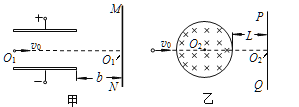
（1）如图甲所示，水平放置的偏转极板的长度为l，板间距为d，极板间的偏转电压为U，在两极板间形成匀强电场。极板右端到竖直荧光屏MN的距离为b，荧光屏MN与两极板间的中心线O1O1′垂直。电子以水平初速度v0从两极板左端沿两极板间的中心线射入，忽略极板间匀强电场的边缘效应，求电子打到荧光屏上时沿垂直于极板板面方向偏移的距离；
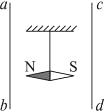
（2）如图乙所示，圆心为O2、半径为r的水平圆形区域中有垂直纸面向里、磁感应强度为B的匀强磁场，与磁场区域右侧边缘的最短距离为L的O2＇处有一竖直放置的荧光屏PQ，荧光屏PQ与O2O2＇连线垂直。今有一电子以水平初速度v0从左侧沿O2O2＇方向射入磁场，飞出磁场区域时其运动方向的偏转角度为α（未知）。请求出
的表达式；
（3）对比第（1）、（2）问中这两种偏转，请从运动情况、受力情况、能量变化情况等角度简要说明这两种偏转的不同点是什么？（至少说出两点）
【答案】（1）
（2）
（3）见解析。
【解析】
试题分析：（1）设电子在偏转电场运动的加速度为a，时间为t，
离开偏转电场时的偏移距离为y，根据运动学公式有：
根据牛顿第二定律有：
电子在电场中的运动时间：
联立解得：
电子飞出偏转电场时，其速度的反向延长线通过偏转电场的中心，
设电子打在屏上距O1′的最大距离为
，则由几何关系可知：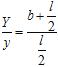
将y代入解得
（2）由牛顿第二定律和洛伦兹力公式得 
解得
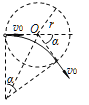
由如图所示的几何关系得，粒子在磁场中一段圆弧轨迹所对应的圆心角与偏转角相等，均为
则：
（3）不同点有：①电子运动类型不同：在电场中电子是匀变速曲线运动，在磁场中电子是匀速圆周运动
②电子受力情况不同：在电场中电子受到的电场力是恒力，在磁场中电子受到的洛伦兹力是大小不变、方向不断变化的变力
③电子速度变化情况不同：在电场中电子速度的大小和方向都发生变化，在磁场中电子速度的大小不改变，仅方向发生变化
④电子运动方向的偏转角范围不同：在电场中电子运动方向的偏转角度一定小于90，在磁场中电子运动方向的偏转角度可能大于90
⑤电子受力做功不同：在电场中电子所受的电场力做正功，在磁场中电子所受的洛伦兹力不做功
⑥电子能量变化情况不同：在电场中电场力做正功，电子动能增加，在磁场中洛伦兹力不做功，电子动能不变（答对一条给2分，最多给4分）
