题目内容
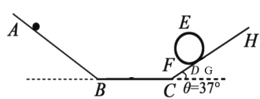
【题目】如图所示,光滑轨道槽ABCD与粗糙轨道槽GH通过光滑圆轨道EF平滑连接(D、G处在同一高度),组成一套完整的轨道,整个装置位于竖直平面内。现将一质量m=1kg的小球从AB段距地面高h0=2m处静止释放,小球滑上右边斜面轨道并能通过轨道的最高点E点。已知CD、GH与水平面的夹角为θ=37°,GH段的动摩擦因数为μ=0.25,圆轨道的半径R=0.4m,E点离水平面的竖直高度为3R(E点为轨道的最高点),(g=10m/s2,sin37°=0.6,cos37°=0.8)求:
(1)小球第一次通过E点时的速度大小;
(2)小球沿GH段向上滑行后距离地面的最大高度;
(3)若小球从AB段离地面h处自由释放后,小球又能沿原路径返回AB段,试求h的取值范围。
【答案】(1)4m/s(2)1.62m;(3)h≤0.8m或h≥2.32m
【解析】
(1)小球从A点到E点由机械能守恒定律可得:![]()
解得:![]()
(2)D、G离地面的高度![]()
设小球在CH斜面上滑的最大高度为hm,则小球从A点滑至最高点的过程,
由动能定理得![]()
由以上各式并代入数据![]()
(3)①小球要沿原路径返回,若未能完成圆周运动,则![]()
②若能完成圆周运动,则小球返回时必须能经过圆轨道的最高点E,在E点,![]()
此情况对应小球在CH斜面上升的高度为![]() ,小球从释放位置滑至最高点的过程,根据动能定理得:
,小球从释放位置滑至最高点的过程,根据动能定理得:![]()
小球从最高点返回E点的过程,根据动能定理得:![]()
由以上各式得h=2.32m
故小球沿原路径返回的条件为h≤0.8m或h≥2.32m

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目