题目内容
【题目】如图所示,有一盛满清水的足够大的池子,水深为d,底面能够反光,一束红色激光以45°的入射角从Q点射入水中,经底面反射后,从水面上P点射出。已知P、Q间的距离为![]() ,真空中的光速为c。
,真空中的光速为c。
①求光在水中的传播速度;
②改变从Q点入射的光的入射角,P点的位置也随之发生移动,则P、Q间的最大距离等于多少?

【答案】(1)![]() ;(2)2d
;(2)2d
【解析】试题分析:①由几何关系求出折射角,由折射定律求解出折射率n,光在水中传播的速度由公式![]() ;②当光线的入射角为90°时,折射角最大,P、Q间的距离最远,由折射定律求出最大的折射角,再由几何关系求出P、Q间的最大距离.
;②当光线的入射角为90°时,折射角最大,P、Q间的距离最远,由折射定律求出最大的折射角,再由几何关系求出P、Q间的最大距离.
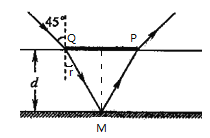
①设光在水的上表面折射角为r。由几何关系可知: 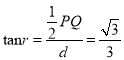
解得r=30°
则![]()
由折射定律得水的折射率为![]()
光在水中的传播速度为![]()
②当光的入射角为90°时,折射角最大,光线离开水面的位置与进入水面的位置间距最远,此时由折射定律有: ![]()
解得![]()
此时PQ的长度![]()

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目