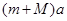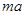题目内容
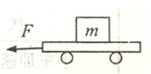
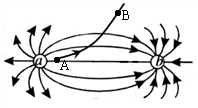
如图所示,小球m1沿半径为R的1/4光滑圆弧从顶端A点由静止运动到最低点B时,与小球m2碰撞并粘在一起沿光滑圆弧末端水平飞出,最终落至C点。已知m1=m2=m,重力加速度为g,两球均可视为质点,C点比B点低4R。求

(1) 小球m1在与小球m2碰撞之前瞬间,m1对圆弧轨道最低点B的压力;
(2) 两球落地点C 与O 点的水平距离S。

(1) 小球m1在与小球m2碰撞之前瞬间,m1对圆弧轨道最低点B的压力;
(2) 两球落地点C 与O 点的水平距离S。
(1)N/=3mg,方向竖直向下; (2)S=2R.
试题分析:小球m1先做圆周运动,运动过程中机械能守恒。m1与m2发生完全非弹性碰撞后一起做平抛运动。
(1)小球m1从A→B由机械能守恒定律
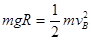 (1)
(1) 小球m1通过最低点B与小球m2碰撞之前时,
由牛顿笫二定律有
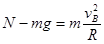 (2)
(2)由牛顿笫三定律有
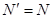 (3)
(3) 由以上三式得: m1对圆弧轨道最低点B的压力为3mg,方向竖直向下
(2) 小球m1与小球m2碰撞并粘在一起,
根据动量守恒定律得
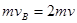 (4)
(4)小球m1与小球m2碰撞后做平抛运动,则水平方向
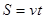 (5)
(5)竖直方向有
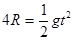 (6)
(6) 由上三式得S=2R。

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
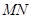 、
、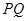 相距为
相距为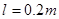 ,三根质量均为
,三根质量均为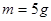 的导体棒
的导体棒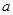 、
、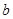 、
、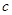 相距一定距离垂直放在导轨上且与导轨间动摩擦因数均为
相距一定距离垂直放在导轨上且与导轨间动摩擦因数均为 ,导体棒
,导体棒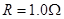 ,导体棒
,导体棒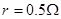 。有磁感应强度为
。有磁感应强度为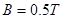 的范围足够大的匀强磁场垂直于导轨平面方向向上。现用一平行于导轨水平向右的足够大的拉力F作用在导体棒
的范围足够大的匀强磁场垂直于导轨平面方向向上。现用一平行于导轨水平向右的足够大的拉力F作用在导体棒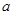 上,使之由静止开始向右做加速运动,导体棒始终与导轨垂直且接触良好,设最大静摩擦力等于滑动摩擦力,忽略导体棒间的相互作用,求:
上,使之由静止开始向右做加速运动,导体棒始终与导轨垂直且接触良好,设最大静摩擦力等于滑动摩擦力,忽略导体棒间的相互作用,求: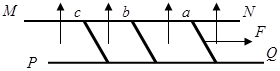
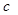 刚开始运动时,导体棒
刚开始运动时,导体棒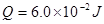 ,撤去拉力F后导体棒
,撤去拉力F后导体棒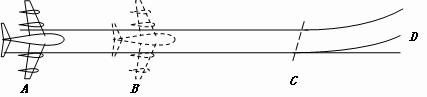
 .则在运动过程中
.则在运动过程中