题目内容
11. 光滑的水平面上,用弹簧相连的质量均为2kg的A、B两物块都以v0=6m/s的速度向右运动,弹簧处于原长,质量为4kg的物块C静止在前方,如图所示.B与C碰撞后二者粘在一起运动,在以后的运动中,当弹簧的弹性势能达到最大时( )
光滑的水平面上,用弹簧相连的质量均为2kg的A、B两物块都以v0=6m/s的速度向右运动,弹簧处于原长,质量为4kg的物块C静止在前方,如图所示.B与C碰撞后二者粘在一起运动,在以后的运动中,当弹簧的弹性势能达到最大时( )| A. | 弹簧的弹性势能最大为EP=10 J | B. | 弹簧的弹性势能最大为EP=12 J | ||
| C. | 物块A的速度是3 m/s | D. | 物块A的速度是6m/s |
分析 B与C发生碰撞后,B的速度减小,碰后BC一起向右运动.A物体没有参加碰撞,速度不变,继续向右运动,这样弹簧被压缩,当三者速度相同时,弹簧压缩量最大,弹性势能最大,根据动量守恒定律求出物体A的速度.根据动量守恒求出B、C碰撞后的共同速度.再由机械能守恒求解弹性势能的最大值.
解答 解:当A、B、C三者的速度相等时弹簧的弹性势能最大.由A、B、C三者组成的系统,取水平向右为正方向,由动量守恒定律得:
(mA+mB)v0=(mA+mB+mC)vA
代入数据解得:物块A的速度 vA=3m/s
B、C碰撞时,B、C系统动量守恒,设碰后瞬间两者的速度为v1,则:
mBv0=(mB+mC)v1
解得:v1=2m/s
设弹簧的弹性势能最大为EP,对碰后过程,根据机械能守恒定律得:
EP=$\frac{1}{2}$(mB+mC)${v}_{1}^{2}$+$\frac{1}{2}$mAv02-$\frac{1}{2}$(mA+mB+mC)vA2.
代入解得为:EP=12J.
故选:BC
点评 本题是含有非弹性碰撞的过程,要分过程研究,不能全过程列出机械能守恒方程:EP=$\frac{1}{2}$(mA+mB)v02-$\frac{1}{2}$(mA+mB+mC)vA2,这是学生经常犯的错误.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
2.一辆动电车做直线运动,速度随时间变化的函数关系为v=bt,其中b=0.3m/s2时( )
| A. | 电动车做匀速直线运动 | B. | 电动车做匀变速直线运动 | ||
| C. | 电动车初速度为0 | D. | 电动车的速度变化量是0.3 m/s |
19.某物体从以10m/s出发,在直线上匀变速前进,已知物体末速度大小为30m/s,所用时间为10s,则加速度a的大小可能是( )
| A. | a=2 | B. | a=-2 | C. | a=-4 | D. | a=4 |
1.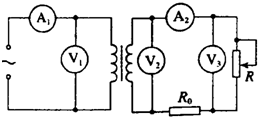 如图所示为街头变压器通过降压给用户供电的示意图,输入电压基本不会变化.输出电压通过输电线输送给用户,两条输电线的总电阻用R0表示,变阻器R代表用户用电器的总电阻,当用电器增加时,相当于R值减小(滑片下移).如果变压器视为理想变压器,A1、A2为理想交流电流表,V1、V2、V3为理想交流电压表,当用电器数量变化时,下列说法正确的是( )
如图所示为街头变压器通过降压给用户供电的示意图,输入电压基本不会变化.输出电压通过输电线输送给用户,两条输电线的总电阻用R0表示,变阻器R代表用户用电器的总电阻,当用电器增加时,相当于R值减小(滑片下移).如果变压器视为理想变压器,A1、A2为理想交流电流表,V1、V2、V3为理想交流电压表,当用电器数量变化时,下列说法正确的是( )
 如图所示为街头变压器通过降压给用户供电的示意图,输入电压基本不会变化.输出电压通过输电线输送给用户,两条输电线的总电阻用R0表示,变阻器R代表用户用电器的总电阻,当用电器增加时,相当于R值减小(滑片下移).如果变压器视为理想变压器,A1、A2为理想交流电流表,V1、V2、V3为理想交流电压表,当用电器数量变化时,下列说法正确的是( )
如图所示为街头变压器通过降压给用户供电的示意图,输入电压基本不会变化.输出电压通过输电线输送给用户,两条输电线的总电阻用R0表示,变阻器R代表用户用电器的总电阻,当用电器增加时,相当于R值减小(滑片下移).如果变压器视为理想变压器,A1、A2为理想交流电流表,V1、V2、V3为理想交流电压表,当用电器数量变化时,下列说法正确的是( )| A. | 用电器增加时,A2示数变大,A1示数变小 | |
| B. | 用电器增加时,V1、V2示数均不变 | |
| C. | 用电器减小时,V3示数变大,A2示数变小 | |
| D. | 用电器减小时,V2示数减小,A1示数变大 |
8.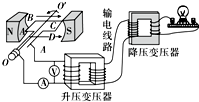 如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$ T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,输电线上损失的功率.导线框及其余导线电阻不计,电表均为理想电表.则下列说法中正确的是( )
如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$ T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,输电线上损失的功率.导线框及其余导线电阻不计,电表均为理想电表.则下列说法中正确的是( )
 如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$ T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,输电线上损失的功率.导线框及其余导线电阻不计,电表均为理想电表.则下列说法中正确的是( )
如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$ T.线框绕垂直于磁场的轴OO′以角速度ω=100π rad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V 1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,输电线上损失的功率.导线框及其余导线电阻不计,电表均为理想电表.则下列说法中正确的是( )| A. | 输电线路的电流为0.98A | |
| B. | 电流表的读数为2.5A | |
| C. | 降压变压器的原副线圈匝数比为5:2 | |
| D. | 线圈从图示位置转过$\frac{π}{2}$的过程中,感应电动势的平均值和有效值之比为$\frac{2\sqrt{2}}{π}$ |
5.一列机械波从一种介质进入另一种介质时,波速变大,则下列判断正确的是( )
| A. | 由v=$\frac{λ}{T}$可知,波长也变大 | |
| B. | 由T=$\frac{λ}{v}$可知,周期变小 | |
| C. | 由v=λf可知,可能是波长λ变小而频率f变得更大 | |
| D. | 由v=λf可知,可能是频率f变小而波长λ变得更大 |
6.如图2甲所示,一个理想变压器原、副线圈的匝数比n1:n2=6:1,副线圈两端接三条支路,每条支路上都接有一只灯泡,电路中L为电感线圈、C为电容器、R为定值电阻.当原线圈两端接有如图2乙所示的交流电时,三只灯泡都能发光.如果加在原线圈两端的交流电的最大值保持不变,而将其频率变为原来的2倍,则对于交流电的频率改变之后与改变前相比,下列说法中正确的是( )
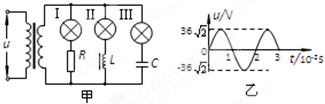

| A. | 副线圈两端的电压有效值均为36V | B. | 副线圈两端的电压有效值均为6V | ||
| C. | 灯泡Ⅰ变亮 | D. | 灯泡Ⅲ变亮 |
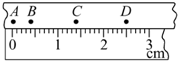 打点计时器每隔0.02 s打一次点,某次实验中得到的一条纸带,用毫米刻度尺测量情况如图所示,纸带在A、C间的平均速度为0.35 m/s,在A、D间的平均速度为0.42m/s,B点的瞬时速度更接近于0.35m/s.(结果保留两位有效数字)
打点计时器每隔0.02 s打一次点,某次实验中得到的一条纸带,用毫米刻度尺测量情况如图所示,纸带在A、C间的平均速度为0.35 m/s,在A、D间的平均速度为0.42m/s,B点的瞬时速度更接近于0.35m/s.(结果保留两位有效数字) 某同学在一楼乘坐电梯上楼,经过7s,电梯恰好到达5楼,整个过程的v-t图象如图所示请根据图象;求:
某同学在一楼乘坐电梯上楼,经过7s,电梯恰好到达5楼,整个过程的v-t图象如图所示请根据图象;求: