题目内容
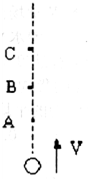 如图所示,将一个物体竖直向上抛出后,上升过程先后经过A、B、C三点,A到B与B到C的间隔距离相等,物体在A、B两点间运动过程动能变化的大小为△Ekl,动量变化的大小为△P1;在B、C两点间运动过程动能变化的大小为△Ek2,动量变化的大小为△P2,若空气阻力恒定,下列关系式中正确的是( )
如图所示,将一个物体竖直向上抛出后,上升过程先后经过A、B、C三点,A到B与B到C的间隔距离相等,物体在A、B两点间运动过程动能变化的大小为△Ekl,动量变化的大小为△P1;在B、C两点间运动过程动能变化的大小为△Ek2,动量变化的大小为△P2,若空气阻力恒定,下列关系式中正确的是( )分析:竖直向上抛出的物体,做匀减速直线运动,根据动能定律可以求得动能的变化,根据动量定理求得动量的变化.
解答:解:(1)竖直向上抛出的物体,向上做匀减速直线运动的过程中,重力和空气的阻力做功,W=(mg+f)h,因空气的阻力不变,hAB=hBC,所以WAB=WBC,
由动能定律可得:W=△EK,所以:△Ekl=△Ek2
(2)上抛的过程中,h=v0t-
at2,得:hAB=vAtA-
a
,hBC=vBtB-
a
因hAB=hBC,vA>vB
所以:tA<tB
A到B的过程:△P1=I1=(mg+f)tA,△P2=I2=(mg+f)tB>△P1.故B正确
故选B
由动能定律可得:W=△EK,所以:△Ekl=△Ek2
(2)上抛的过程中,h=v0t-
| 1 |
| 2 |
| 1 |
| 2 |
| t | 2 A |
| 1 |
| 2 |
| t | 2 B |
因hAB=hBC,vA>vB
所以:tA<tB
A到B的过程:△P1=I1=(mg+f)tA,△P2=I2=(mg+f)tB>△P1.故B正确
故选B
点评:本题主要考查了动量的表达式和动量定理的直接应用,难度不大,属于基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目