题目内容
3.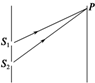 如图所示,在杨氏双缝干涉实验中,S1和S2为双缝,P是光屏上的一点,已知P点与S1、S2的路程差为2.1×10-6m.已知某单色光在折射率为n=1.5的介质中波长为4×10-7m.现用该单色光在空气中做双缝干涉实验,问P点是暗条纹(选填“亮条纹”或“暗条纹”).若将光屏右移,保持其他条件不变,则屏上的条纹间距将变宽(选填“变宽”、“变窄”或“不变”).
如图所示,在杨氏双缝干涉实验中,S1和S2为双缝,P是光屏上的一点,已知P点与S1、S2的路程差为2.1×10-6m.已知某单色光在折射率为n=1.5的介质中波长为4×10-7m.现用该单色光在空气中做双缝干涉实验,问P点是暗条纹(选填“亮条纹”或“暗条纹”).若将光屏右移,保持其他条件不变,则屏上的条纹间距将变宽(选填“变宽”、“变窄”或“不变”).
分析 双缝到光屏上P点的距离之差是波长的整数倍,则出现明条纹,路程之差是半波长的奇数倍,则出现暗条纹;再根据干涉条纹间距公式,即可判定求得.
解答 解:设A光在空气中波长为λ1,在介质中波长为λ2,
由n=$\frac{c}{v}$=$\frac{{λ}_{1}}{{λ}_{2}}$ 得,
λ1=nλ2=1.5×4×10-7m=6×10-7m.
根据光程差:δ=2.1×10-6m=3$\frac{1}{2}$λ1,
知A光在P点是暗条纹.
根据干涉条纹间距公式:$△x=\frac{L}{d}λ$,可知,缝屏间距L变大时,则条纹间距将变宽,
故答案为:暗条纹,变宽.
点评 解决本题的关键掌握双缝到光屏上P点的距离之差是波长的整数倍,则出现明条纹,路程之差是半波长的奇数倍,则出现暗条纹,并掌握干涉条纹间距公式的应用.

练习册系列答案
相关题目
16.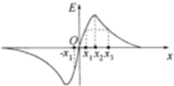 空间有一沿x轴对称分布的电场,电场强度就在x轴上且规定沿x轴正向为正,其电场强度E随x轴变化的图象如图所示,图象过坐标原点O点,下列说法中正确的是( )
空间有一沿x轴对称分布的电场,电场强度就在x轴上且规定沿x轴正向为正,其电场强度E随x轴变化的图象如图所示,图象过坐标原点O点,下列说法中正确的是( )
 空间有一沿x轴对称分布的电场,电场强度就在x轴上且规定沿x轴正向为正,其电场强度E随x轴变化的图象如图所示,图象过坐标原点O点,下列说法中正确的是( )
空间有一沿x轴对称分布的电场,电场强度就在x轴上且规定沿x轴正向为正,其电场强度E随x轴变化的图象如图所示,图象过坐标原点O点,下列说法中正确的是( )| A. | x1和x3两点的电势相等 | |
| B. | 在x轴上场强最大的点有两个,其中一个点是x2 | |
| C. | 坐标原点O点的电势最低 | |
| D. | x1和-x1两点的电势相等 |
17.一列简谐横波在x轴上传播,波源处于x=0m处,在x=3m处的质元P和x=6m处的质元Q的振动图线分别如图甲、乙所示,下列说法正确的( )


| A. | 波长可能是4m | B. | 波的周期一定是12s | ||
| C. | 波的振幅一定是8cm | D. | 波的传播速度一定是1m/s | ||
| E. | 波由P传播到Q历时可能是9s |
11.下列说法正确的是( )
| A. | 太阳辐射的能量主要来自太阳内部的核聚变反应 | |
| B. | 汤姆孙通过对阴极射线的研究发现了电子,说明原子是有复杂结构的 | |
| C. | 卢瑟福发现了中子、查德威克发现了质子 | |
| D. | 一束光照射到某金属上不能发生光电效应,是因为该束光的波长太短 | |
| E. | 按照波尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,原子总能量增大 |
18.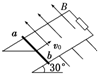 一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则金属杆在滑行过程中( )
一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则金属杆在滑行过程中( )
 一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则金属杆在滑行过程中( )
一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则金属杆在滑行过程中( )| A. | 向上滑行的时间小于向下滑行的时间 | |
| B. | 在向上滑行时电阻R上产生的热量大于向下滑行时电阻R上产生的热量 | |
| C. | 向上滑行时与向下滑行时通过电阻R的电荷量相等 | |
| D. | 金属杆从开始上滑至返回出发点,电阻R上产生的热量为$\frac{1}{2}$m(v02-v2) |
8.关于振动和波的关系,下列说法中正确的是( )
| A. | 有机械波就一定有机械振动 | |
| B. | 有机械振动就一定有机械波 | |
| C. | 如果波源停止振动,波也立即停止向前传播 | |
| D. | 机械波传播过程中,质点将沿波的传播方向平移 |
12.1905年3月,爱因斯坦提出狭义相对性原理,开创了物理学的新纪元,下列属于狭义相对论基本假设的是:在不同的惯性系中( )
| A. | 物体的质量不变 | B. | 真空中光速不变 | ||
| C. | 时间间隔具有相对性 | D. | 物体的能量与质量成正比 |