题目内容
在考古中为了测定古物的年代,可通过测定古物中碳14与碳12的比例,其物理过程可简化为如图所示.碳14与碳12经电离后的原子核带电量都为q,由静止经电压U加速后从O点进人磁感应强度为B的匀强磁场,OM为磁场的下边界线,可在OM上适当位置放置粒子记数器,从而测定碳14与碳12的比例(不计粒子的重力及粒子间的相互作用力).求:(1)碳14与碳12在磁场中运动的半径比
(2)在实际中并不是所有粒子都垂直于OM沿ON射入磁场,而是分布在与ON成一定夹角θ的纸面内,要使两种粒子运动到OM直线上时能区分在不同区域,θ角的范围;
(3)θ取最大时,用阴影表示出碳14粒子在磁场中可能出现的区域.

【答案】分析:(1)根据动能定理以及带电粒子所受的洛伦兹力提供向心力,得出轨道半径的表达式,抓住两粒子电量相同,质量不同,求出运动的半径之比.
(2)碳14的轨道半径大于碳12的轨道半径,要使两种粒子运动到OM直线上时能区分在不同区域,使得碳14在OM上最近距离大于碳12的最远距离.根据结合关系,结合半径公式求出θ角的范围.
(3)分别作出两个速度方向与竖直方向成θ角的两个圆弧的轨迹,确定两个临界状态下粒子走过的轨迹,通过粒子圆弧的直径大小不变,当速度角度变化时,确定出碳14粒子在磁场中可能出现的区域.
解答:解:(1)原子核经电场加速有:qU=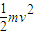 .
.
在磁场中做圆周运动有: .
.
则R= .
.
则碳14和碳12在磁场中运动的半径比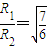 .
.
(2)碳14在OM上运动的最近距离为L1=2R1cosθ
碳12在OM上运动的最远距离为L2=2R2.
要使两种粒子运动到OM直线上时能区分在不同区域,则L1≥L2
 .
.
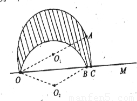
(3)碳14粒子在磁场中可能出现的区域如图所示.
(OA弧是以O1为圆心,半径为R1的半圆弧;AC弧是以O为圆心半径为2R1的圆弧;OB弧是以O2为圆心半径为R1的圆弧)
 答:(1)碳14与碳12在磁场中运动的半径比为
答:(1)碳14与碳12在磁场中运动的半径比为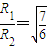 .
.
(2)要使两种粒子运动到OM直线上时能区分在不同区域,θ角的范围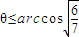 .
.
(3)碳14粒子在磁场中可能出现的区域如图所示.
点评:此题的关键是能找到临界条件,根据临界条件列式求解.同时要熟练掌握磁场中洛伦兹力提供向心力,画出圆弧,是道难题.
(2)碳14的轨道半径大于碳12的轨道半径,要使两种粒子运动到OM直线上时能区分在不同区域,使得碳14在OM上最近距离大于碳12的最远距离.根据结合关系,结合半径公式求出θ角的范围.
(3)分别作出两个速度方向与竖直方向成θ角的两个圆弧的轨迹,确定两个临界状态下粒子走过的轨迹,通过粒子圆弧的直径大小不变,当速度角度变化时,确定出碳14粒子在磁场中可能出现的区域.
解答:解:(1)原子核经电场加速有:qU=
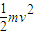 .
.在磁场中做圆周运动有:
 .
.则R=
 .
.则碳14和碳12在磁场中运动的半径比
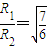 .
.(2)碳14在OM上运动的最近距离为L1=2R1cosθ
碳12在OM上运动的最远距离为L2=2R2.
要使两种粒子运动到OM直线上时能区分在不同区域,则L1≥L2
 .
.(3)碳14粒子在磁场中可能出现的区域如图所示.
(OA弧是以O1为圆心,半径为R1的半圆弧;AC弧是以O为圆心半径为2R1的圆弧;OB弧是以O2为圆心半径为R1的圆弧)
 答:(1)碳14与碳12在磁场中运动的半径比为
答:(1)碳14与碳12在磁场中运动的半径比为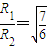 .
.(2)要使两种粒子运动到OM直线上时能区分在不同区域,θ角的范围
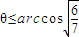 .
.(3)碳14粒子在磁场中可能出现的区域如图所示.
点评:此题的关键是能找到临界条件,根据临界条件列式求解.同时要熟练掌握磁场中洛伦兹力提供向心力,画出圆弧,是道难题.

练习册系列答案
相关题目
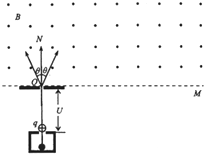 在考古中为了测定古物的年代,可通过测定古物中碳14与碳12的比例,其物理过程可简化为如图所示.碳14与碳12经电离后的原子核带电量都为q,由静止经电压U加速后从O点进人磁感应强度为B的匀强磁场,OM为磁场的下边界线,可在OM上适当位置放置粒子记数器,从而测定碳14与碳12的比例(不计粒子的重力及粒子间的相互作用力).求:
在考古中为了测定古物的年代,可通过测定古物中碳14与碳12的比例,其物理过程可简化为如图所示.碳14与碳12经电离后的原子核带电量都为q,由静止经电压U加速后从O点进人磁感应强度为B的匀强磁场,OM为磁场的下边界线,可在OM上适当位置放置粒子记数器,从而测定碳14与碳12的比例(不计粒子的重力及粒子间的相互作用力).求:
