题目内容
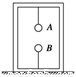
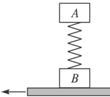如图所示，A、B两木块间连一轻质弹簧，A、B质量相等，一起静止地放在一块木板上．若将此木板突然抽去，在此瞬间，A、B两木块的加速度分别是（ ）分析：木板抽出前，木块A和木块B都受力平衡，根据共点力平衡条件求出各个力；木板抽出后，木板对木块B的支持力突然减小为零，其余力均不变，根据牛顿第二定律可求出两个木块的加速度．
解答：解：在抽出木板的瞬时，弹簧对A的支持力和对B的压力并未改变．对A物体受重力和支持力，mg=F，aA=0．
对B物体受重力和弹簧的向下的压力，根据牛顿第二定律a=
=
=2g
故选A
对B物体受重力和弹簧的向下的压力，根据牛顿第二定律a=
| F+mg |
| m |
| mg+mg |
| m |
故选A
点评：本题属于牛顿第二定律应用的瞬时加速度问题，关键是区分瞬时力与延时力；弹簧的弹力通常来不及变化，为延时力，轻绳的弹力为瞬时力，绳子断开即消失．
练习册系列答案
相关题目
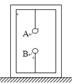
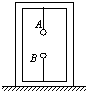（2011?徐州模拟）如图所示，A，B两个带有异种电荷的小球分别被两根绝缘细线系在木盒内，且在同一竖直线上，静止时木盒对地面的压力为FN，细线对B的拉力为F．若将系B的细线断开，下列说法中正确的是（ ）
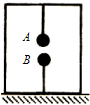（2008?江苏模拟）如图所示，A、B两个带异种电荷的小球分别被两根绝缘细线系在一放在水平支持面上的木盒内的顶部和底部，木盒对地面的压力为N，细线对球B拉力为F．若将系B的细线断开，（ ）
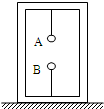如图所示，A、B两个异种电荷的等质量小球，分别被两根绝缘细绳系在木盒内的同一竖直线上．静止时，木盒对地面的压力为FN，细绳对A的拉力为F1，细绳对B的拉力为F2，若将系B的细绳和系A的细绳同时断开，则两细绳刚断开时（ ）
