Question

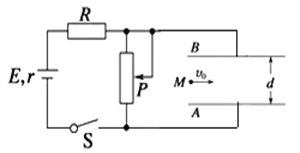
【题目】如图所示，水平地面上有一质量为M=2m的箱子，在水平向右的拉力作用下，以速率v0向右做匀速直线运动，箱内底面上紧靠左端面处有一质量为m光滑的小球，小球到车右端面的距离为L，箱子与地面之间动摩擦因数为μ。某时刻撤去水平拉力，经一段时间小球与车的右端面相撞。已知小球与箱子碰撞时间极短且碰撞后不再分离，重力加速度g。求：

（1）撤去水平向右的拉力时，箱子的加速度大小a1；

（2）初速度v0满足什么关系时，小球与箱子右端碰撞前箱子已经停下；

（3）当时，箱子向右运动的总位移s。

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）对箱子：其受力图如图所示

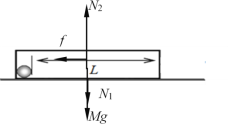
由牛顿第二定律得

f=Ma1①

N2=N1+Mg②

由摩擦力公式得

f=μN2③

对小球：地面对它支持力

N1′=mg④

由牛顿第三定律得

N1=N1′，方向相反⑤

由①②③④⑤得

⑥

（2）若小球未与箱子右端面相碰前箱子停下，设箱子运动s1距离停下，所用时间为t1，由运动学公式有

⑦

⑧

设这段时间小球运动位移s2，则

⑨

这段时间内小球相对箱子移动的距离

⑩

依题意得

Δs≤L

由⑩得

（3）当时，小球与箱子右端面相碰前，箱子未停下。设经过时间t1′小球与箱子右端面相碰，此过程箱子运动位移为s1′，碰前速度为v1，碰后共同速度为v，由运动学公式

这段时间内小球位移

s2′=v0t1′

依题意得

s2′-s1′=L

小球与箱子相碰过程系统动量守恒

mv0+Mv1=(m+M)v

设：此后小球与箱子一起运动的位移为s1″，由动能定理得

所以箱子向右运动的总位移

由⑥解得